
【题目】梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 在
在![]() 上,
上,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 和
和![]() 分别与
分别与![]() 交于
交于![]() 和
和![]() ,
,![]() 和
和![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 在四边形
在四边形![]() 内部时,设
内部时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)![]()
![]() ;(3)3或
;(3)3或![]() .
.
【解析】
(1)由中位线的性质,角平分线的定义和平行线的性质得出![]() ,易证
,易证![]() ,则结论可证;
,则结论可证;
(2)过![]() 作
作![]() 交
交![]() 于点K,过点D作
于点K,过点D作![]() 交
交![]() 于点
于点![]() ,则得到矩形
,则得到矩形![]() ,则有
,则有![]() ,
,![]() ,然后利用(1)中的结论有
,然后利用(1)中的结论有![]() ,
, ![]() ,在
,在![]() 中,利用含30°的直角三角形的性质可得出QC,DQ的长度,然后在
中,利用含30°的直角三角形的性质可得出QC,DQ的长度,然后在![]() 中利用勾股定理即可找到y关于x的函数关系式;
中利用勾股定理即可找到y关于x的函数关系式;
(3)分两种情况:点![]() 在梯形
在梯形![]() 内部和点
内部和点![]() 在梯形
在梯形![]() 内部,当点
内部,当点![]() 在梯形
在梯形![]() 内部时,有
内部时,有![]() ;当点
;当点![]() 在梯形
在梯形![]() 内部时,有
内部时,有![]() ,分别结论(2)中的关系式即可求出EG的长度.
,分别结论(2)中的关系式即可求出EG的长度.
(1)证明:![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
![]() .
.
![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]() .
.
![]() .
.
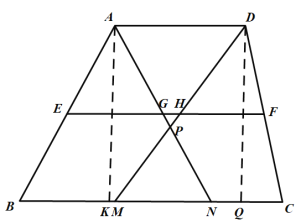
(2)过![]() 作
作![]() 交
交![]() 于点K,过点D作
于点K,过点D作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是矩形,
是矩形,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
同理:![]() .
.
在![]() 中,
中,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() .
.
![]() ,
,
即![]() .
.
![]()
![]() .
.
(3)①点![]() 在梯形
在梯形![]() 内部.
内部.
∵![]() 是梯形
是梯形![]() 的中位线,
的中位线,
![]() ,
,
即![]() .
.
解得:![]() ,
,
即![]() .
.
②点![]() 在梯形
在梯形![]() 内部.
内部.
同理:![]() .
.
解得:![]() ,
,
即![]() .
.
综上所述,EG的长度为3或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知a是大于1的实数,且有a3+a-3=p,a3-a-3=q.
(1)若p+q=4,求p-q的值;
(2)当q2=22n+![]() -2(n≥1,且n是整数)时,比较p与a3+
-2(n≥1,且n是整数)时,比较p与a3+![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2700元购进甲、乙两种商品共100件,这两种商品的进价、标价如下表所示:
| 甲种 | 乙种 |
进价(元/件) | 15 | 35 |
标价(元/件) | 20 | 45 |
(1)求购进两种商品各多少件?
(2)商品将两种商品全部卖出后,获得的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩 形,这样的矩形称为叠合矩形.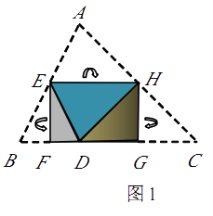
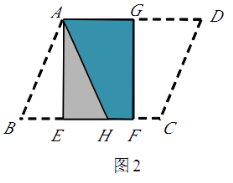

(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 , ;S矩形AEFG:S□ABCD=
(2)ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长.
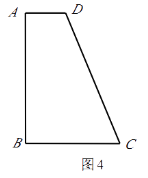
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出AD,BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
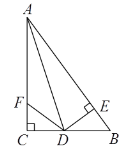
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对代数式![]() ,老师要求任意取一个x的值后求出代数式的值.圆圆发现,大家所求得的代数式的值都大于等于0,即x=-3时代数式的最小值是0.利用这个发现,圆圆试着写出另外一些结论:①在x=-3时,代数式(x+3)2+2的最小值为2;②在a=-b时,代数式(a+b)2+m的最小值为m;③在c=-d时,代数式-(c+d)2+n的最大值为n;④在
,老师要求任意取一个x的值后求出代数式的值.圆圆发现,大家所求得的代数式的值都大于等于0,即x=-3时代数式的最小值是0.利用这个发现,圆圆试着写出另外一些结论:①在x=-3时,代数式(x+3)2+2的最小值为2;②在a=-b时,代数式(a+b)2+m的最小值为m;③在c=-d时,代数式-(c+d)2+n的最大值为n;④在![]() 时,代数式
时,代数式![]() 的最大值为29.其中正确的为( )
的最大值为29.其中正确的为( )
A. ①②③B. ①③C. ①④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC= ![]() ,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是( )
,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:12:00时是一个两位数,数字之和为7;13:00时十位与个位数字与12:00是所看到的正好互换了;14:00时比12:00时看到的两位数中间多出一个0.如果设小明在12:00看到的数的十位数字是x,个位数字是y,根据题意可列方程组为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com