
【题目】如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
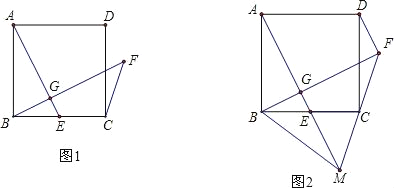
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
试题分析:(1)过C点作CH⊥BF于H点,根据已知条件可证明△AGB≌△BHC,所以AG=BH,BG=CH,又因为BH=BG+GH,所以可得BH=HF+GH=FG,进而证明AG=FG;
(2)过D作DQ⊥MF交MF延长线于Q,根据全等三角形的性质和等腰三角形的性质即可求出FD的长.
试题解析:(1)过C点作CH⊥BF于H点,
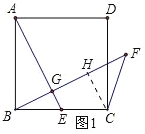
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC,
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
(2)∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=![]() GM,
GM,
∴BG=![]() GM,
GM,
∵BM=10,
∴BG=2![]() ,GM=4
,GM=4![]() ,
,
∴AG=4![]() ,AB=10,
,AB=10,
∴HF=2![]() ,
,
∴CF=2![]() ×
×![]() =2
=2![]() ,
,
∴CM=2![]() ,
,
过B点作BK⊥CM于K,
∵CK=![]() CM=
CM=![]() CF=
CF=![]() ,
,
∴BK=3![]() ,
,
过D作DQ⊥MF交MF延长线于Q,
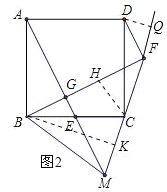
∴△BKC≌△CQD
∴CQ=BK=3![]() ,
,
DQ=CK=![]() ,
,
∴QF=3![]() -2
-2![]() =
=![]() ,
,
∴DF=![]() =2
=2![]() .
.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题是( )
A.等腰三角形两腰上的高相等
B.面积相等的两个三角形全等
C.两条直线被第三条直线所截,内错角相等
D.一个角的两边与另一个角的两边分别平行,那么这两个角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组线段中,能成比例的是( )
A. 1㎝,3㎝,4㎝,6㎝ B. 30㎝,12㎝,0.8㎝,0.2㎝
C. 0.1㎝,0.2㎝,0.3㎝,0.4㎝ D. 12㎝,16㎝,45㎝,60㎝
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校2000名学生的身高情况,随机抽取了该校200名学生测量身高.在这个问题中,样本容量是( )
A. 2000名学生 B. 2000 C. 200名学生 D. 200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是平行投影
B. 平行投影一定是太阳光照射下的
C. 物体的主视图实际上就是该物体在某一平行光线下的投影
D. 不同时刻,大树和小树的影长与它们的高度成正比例关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P为直线l外一点,点A,B,C为直线l上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线l的距离为( )
A. 5 cm B. 4 cm C. 2 cm D. 不大于2 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名管理人员,对甲、乙两名竞聘者进行了两项测试,各项测试成绩如下表:
测试项目 | 测试成绩(分) | |
甲 | 乙 | |
笔试 | 75 | 84 |
面试 | 88 | 72 |
公司将笔试、面试两项测试成绩分别以60%、40%记入个人最后成绩,并根据成绩择优录用,你认为谁将被录用?(要求写出计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
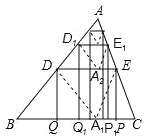
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com