
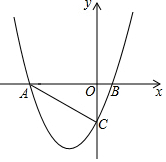
 如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.
如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.分析 (1)先确定C(0,-2),设交点式y=a(x+4)(x-1),然后把C点坐标代入求出a即可得到抛物线的解析式;
(2)先利用待定系数法确定直线BC的解析式为y=2x-2,设D(m,2m-2),讨论:当BD=BA时,利用两点间的距离公式得到(m-1)2+(2m-2)2=52,当AD=AB时,利用两点的距离公式得到(m+4)2+(2m-2)2=52,然后分别解方程求出m即可得到满足条件的D点坐标;
(3)先利用勾股定理的逆定理证明△ABC为直角三角形,∠ACB=90°,由于△ACO∽△ABC,△APQ与△ABC相似,则只有∠CAP=∠OAC,设直线AP交y轴于E,作CF⊥AE于P,则CF=CO=2,证明△ECF∽△EAO,利用相似比得到$\frac{EC}{EA}$=$\frac{CF}{AO}$=$\frac{1}{2}$,在Rt△AOE中利用勾股定理可计算出CE=$\frac{10}{3}$,则E(0,-$\frac{16}{3}$),再利用待定系数法确定直线AE的解析式为y=-$\frac{4}{3}$x-$\frac{16}{3}$,然后解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}+\frac{3}{2}x-2}\\{y=-\frac{4}{3}x-\frac{16}{3}}\end{array}\right.$可得到P点坐标.
解答 解:(1)∵B(1,0),OC=2OB,
∴C(0,-2),
设抛物线解析式为y=a(x+4)(x-1),
把C(0,-2)代入得a•4•(-1)=-2,解得a=$\frac{1}{2}$,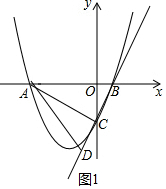
∴抛物线的解析式为y=$\frac{1}{2}$(x+4)(x-1),即y=$\frac{1}{2}$x2+$\frac{3}{2}$x-2;
(2)AB=1-(-4)=5,
设直线BC的解析式为:y=kx+b,
把B(1,0),C(0,-2)代入得$\left\{\begin{array}{l}{k+b=0}\\{b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=-2}\end{array}\right.$,
∴直线BC的解析式为y=2x-2,
设D(m,2m-2),
∵△ABD为以AB为腰的等腰三角形,
∴BD=BA=5或AD=AB=5,
当BD=BA时,即(m-1)2+(2m-2)2=52,解得m1=1+$\sqrt{5}$,m2=1-$\sqrt{5}$,此时D点坐标为(1+$\sqrt{5}$,2$\sqrt{5}$),(1-$\sqrt{5}$,-2$\sqrt{5}$),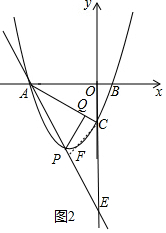
当AD=AB时,即(m+4)2+(2m-2)2=52,解得m1=1(舍去),m2=-1,此时D点坐标为(-1,-4),
综上所述,满足条件的D点坐标为(1+$\sqrt{5}$,2$\sqrt{5}$),(1-$\sqrt{5}$,-2$\sqrt{5}$),(-1,-4);
(3)AB2=25,BC2=12+22=5,AC2=42+22=20,
∵AB2=BC2+AC2,
∴△ABC为直角三角形,∠ACB=90°,
∵∠BAC=∠CAO,
∴△ACO∽△ABC,
∵△APQ与△ABC相似,
∴∠CAP=∠OAC,
∴AC平分∠BAP,
设直线AP交y轴于E,作CF⊥AE于P,则CF=CO=2,
∵∠CEF=∠AEO,
∴△ECF∽△EAO,
∴$\frac{EC}{EA}$=$\frac{CF}{AO}$=$\frac{2}{4}$=$\frac{1}{2}$,
在Rt△AOE中,∵OE2+OA2=AE2,
∴(2+CE)2+42=(2CE)2,解得CE=-2(舍去)或CE=$\frac{10}{3}$,
∴E(0,-$\frac{16}{3}$),
设直线AE的解析式为y=mx+n,
把A(-4,0),E(0,-$\frac{16}{3}$)得$\left\{\begin{array}{l}{-4m+n=0}\\{n=-\frac{16}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{4}{3}}\\{n=-\frac{16}{3}}\end{array}\right.$,
∴直线AE的解析式为y=-$\frac{4}{3}$x-$\frac{16}{3}$,
解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}+\frac{3}{2}x-2}\\{y=-\frac{4}{3}x-\frac{16}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{5}{3}}\\{y=-\frac{28}{9}}\end{array}\right.$,
∴P(-$\frac{5}{3}$,-$\frac{28}{9}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰三角形的性质;会利用待定系数法求函数解析式;能运用两点间的距离公式和相似比计算线段的长;会运用分类讨论的思想解决数学问题.


科目:初中数学 来源: 题型:解答题
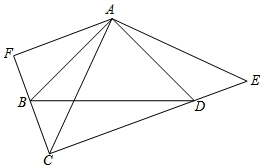 如图,∠BAD=∠CAE=90°,AB=AD,AC=AE,AF⊥CF,垂足为F.
如图,∠BAD=∠CAE=90°,AB=AD,AC=AE,AF⊥CF,垂足为F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com