

 AB;
AB; 的中点,CM交AB于点N,若AB=4,求MN·MC的值.
的中点,CM交AB于点N,若AB=4,求MN·MC的值. AB,证明略。
AB,证明略。 A ,∠COB=2∠PCB
A ,∠COB=2∠PCB  ……………………1分
……………………1分
 (2)∵PC="AC " ∴∠A=∠P
(2)∵PC="AC " ∴∠A=∠P AB ………………………………………………………6分
AB ………………………………………………………6分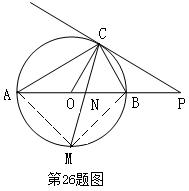
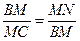
 ,弧AM=弧BM
,弧AM=弧BM 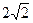 ………………………………………………………9分
………………………………………………………9分

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源:不详 题型:解答题

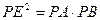 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.点A在⊙O内部 | B.点A在⊙O上 | C.点A在⊙O外部 | D.点A不在⊙O上 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 10 |
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com