

分析 (1)只要证明∠3=∠4,∠BOP=∠PED即可根据AAS证明;
(2)只要证明△ABP≌△CPD,即可推出AP=CD;
解答 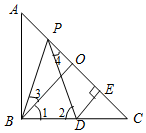 证明:∵PB=PD,
证明:∵PB=PD,
∴∠2=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠A=∠C=45°,
∵AB=BC,BO中线,
∴BO⊥AC,∠1=$\frac{1}{2}∠ABC$=45°,
∴∠1=∠C,
∵∠PBC=∠3+∠1,∠2=∠4+∠C,
∴∠3=∠4,.
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△BPO和△PDE中
$\left\{\begin{array}{l}{∠3=∠4}\\{∠BOP=∠PED}\\{BP=PD}\end{array}\right.$,
∴△BPO≌△PDE(AAS);
(2)证明:由(1)可得:∠3=∠4,
∵BP平分∠ABO,
∴∠ABP=∠3,
∴∠ABP=∠4,
在△ABP和△CPD中
$\left\{\begin{array}{l}{∠A=∠C}\\{∠ABP=∠4}\\{PB=PD}\end{array}\right.$,
∴△ABP≌△CPD,
∴AP=CD.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、直角三角形斜边中线的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚普通正六面体骰子所得点数不超过6 | |
| B. | 买一张体育彩票中一等奖 | |
| C. | 从实数-$\frac{2}{7},\sqrt{3},\root{3}{-8},\frac{1}{3}$π,0.1010010001中随机抽取一个数恰好是有理数 | |
| D. | 口袋中装有10 个红球,从中摸出一个是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )
把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
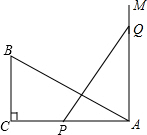 如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由.
如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com