
 如图1,AC⊥CG,AC=
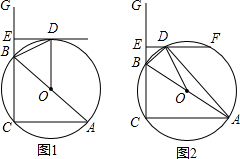
如图1,AC⊥CG,AC= ,B是CG上一动点,将△ABC沿直线AB翻折到△ABD.过D作直线DE⊥CG,垂足为E.
,B是CG上一动点,将△ABC沿直线AB翻折到△ABD.过D作直线DE⊥CG,垂足为E.
 AB,
AB, ,BC=2,
,BC=2, =
= ,
, ∵∠DAF=∠CAB,
∵∠DAF=∠CAB, =
= =
= ,
,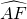 =
= =2
=2 ,
, =4
=4 ,
, =4
=4 =180°,
=180°, =45°,
=45°, ×(
×( -1)=2
-1)=2 -2
-2 .
. AB,得出点D在⊙O上,再根据cot∠CAB=
AB,得出点D在⊙O上,再根据cot∠CAB= =
= ,得出∠CAB=∠BAD=30°,从而求出∠ABC=∠ABD=60°;
,得出∠CAB=∠BAD=30°,从而求出∠ABC=∠ABD=60°; =
= =
= ,再根据CG⊥DF,AC⊥CG,得出DF∥AC,
,再根据CG⊥DF,AC⊥CG,得出DF∥AC, =
= =2
=2 ,
, =4
=4 ,最后根据
,最后根据 =4
=4 =180°,
=180°, =45°,求出∠CAB=22.5°,BC=AC×tan22.5°.
=45°,求出∠CAB=22.5°,BC=AC×tan22.5°.

 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江伊春区九年级上学期期末检测数学试卷(解析版) 题型:解答题
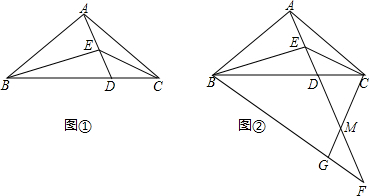
已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时(如图1)易证:AB=CG+CE.
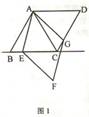
(1)当点在E线段BC的延长线上时(如图2),猜想AB、CG、CE之间的关系并证明;
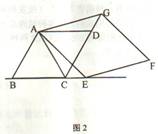
(2)当点在E线段CB的延长线上时(如图3),猜想AB、CG、CE之间的关系.
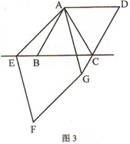
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com