
【题目】已知![]() 中,
中, ![]() ,
, ![]() .如图,将
.如图,将![]() 进行折叠,使点
进行折叠,使点![]() 落在线段
落在线段![]() 上(包括点
上(包括点![]() 和点
和点![]() ),设点
),设点![]() 的落点为
的落点为![]() ,折痕为
,折痕为![]() ,当
,当![]() 是等腰三角形时,点
是等腰三角形时,点![]() 可能的位置共有( ).
可能的位置共有( ).

A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号![]() 表示不大于
表示不大于![]() 的最大整数,称
的最大整数,称![]() 为a的根整数,例如:
为a的根整数,例如: ![]() ,
, ![]() .
.
(1)仿照以上方法计算: ![]() = ;
= ; ![]() = .
= .
(2)若![]() =1,写出满足题意的x的整数值 .
=1,写出满足题意的x的整数值 .
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 ![]() ,这时候结果为1.
,这时候结果为1.
(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,∠A=∠F,试说明∠C=∠D.
解:∵∠1=∠2 (已知 )
∠1=∠ ( )
∴∠2=∠ (等量代换)
∴BD∥ ( )
∴∠ABD=∠ (两直线平行,同位角相等)
∵∠A=∠F ( 已知 )
∴DF∥ ( )
∴∠ABD=∠ (两直线平行,内错角相等)
∴∠C=∠D ( ).
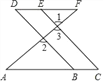
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG;(2)OG= ![]() BC;(3)△OGE是等边三角形;(4)
BC;(3)△OGE是等边三角形;(4)![]() .
.
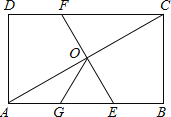
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是一张等腰直角三角形纸板,
是一张等腰直角三角形纸板, ![]() ,
, ![]() .
.
(![]() )要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图
)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图![]() ),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
(![]() )图
)图![]() 中甲种剪法称为第
中甲种剪法称为第![]() 次剪取,记所得正方形面积为
次剪取,记所得正方形面积为![]() ;按照甲种剪法,在余下的
;按照甲种剪法,在余下的![]() 和
和![]() 中,分别剪取正方形,得到两个相同的正方形,称为第
中,分别剪取正方形,得到两个相同的正方形,称为第![]() 次剪取,并记这两个正方形面积和为
次剪取,并记这两个正方形面积和为![]() (如图
(如图![]() ),则
),则![]() __________;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第
__________;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第![]() 次剪取,并记这四个正方形面积和为
次剪取,并记这四个正方形面积和为![]() ,继续操作下去,则第
,继续操作下去,则第![]() 次剪取时,
次剪取时, ![]() __________.
__________.
(![]() )求第
)求第![]() 次剪取后,余下的所有小三角形的面积之和__________.
次剪取后,余下的所有小三角形的面积之和__________.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com