Question

等腰三角形的底边长为2，面积等于1，则它的顶角度数为________．

Answer 1

90°
分析：作出草图，先根据三角形的面积求出底边上的高为1，然后根据等腰三角形三线合一的性质可得底边上的高把三角形分成两个等腰直角三角形，从而得解．
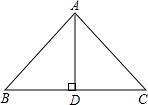
解答：解：如图，设等腰△ABC的底边BC=2，
则BC•AD=1，
即×2•AD=1，
解得AD=1，
∵△ABC是等腰三角形，
∴BD=CD=BC=1，
∴△ABD与△ACD都是等腰直角三角形，
∴∠BAD=∠CAD=45°，
∴∠BAC=45°×2=90°，
即它的顶角度数为90°．
故答案为：90°．
点评：本题主要考查了等腰直角三角形的判定与性质，等腰三角形三线合一的性质，以及三角形的面积，作出图形更形象直观，有助于问题的解决．