
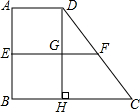
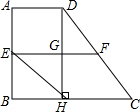
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,CD=4,梯形的高DH与中位线EF交于点G,则下列结论中:
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,CD=4,梯形的高DH与中位线EF交于点G,则下列结论中:| S△DGF |
| S△DHC |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| S△DGF |
| S△DHC |
| GF |
| CH |
| 1 |
| 2 |
| 1 |
| 4 |


科目:初中数学 来源: 题型:
 如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),则可发现“努”的坐标与其有一定的关系,根据其关系,破译“正做数学”的真实意思是
如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),则可发现“努”的坐标与其有一定的关系,根据其关系,破译“正做数学”的真实意思是查看答案和解析>>
科目:初中数学 来源: 题型:
| A、两直线平行,同位角相等 |
| B、两直线平行,内错角相等 |
| C、两三角形全等,三对对应边相等 |
| D、两三角形全等,三对对应角相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com