
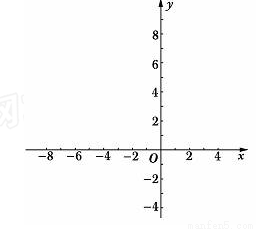
(11分)已知抛物线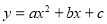
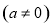 与
与 轴交于A、B两点,与
轴交于A、B两点,与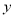 轴交于点C,其中点B在
轴交于点C,其中点B在 轴的正半轴上,点C在
轴的正半轴上,点C在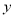 轴的正半轴上,OB=2,OC=8,抛物线的对称轴是直线
轴的正半轴上,OB=2,OC=8,抛物线的对称轴是直线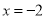 .
.
(1)求此抛物线的表达式;
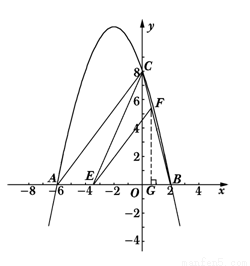
(2)连接AC、BC、,若点E是线段AB上的一个动点(与点A、点B不重合),过点E做EF//AC交与点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(3)在(2)的基础上说明S是否存在最大值,若存在,请求出S的最大值,并求出此点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
(1)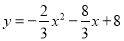 ;(2)
;(2)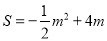 ,(0<m<8);(3)当m=4时,S有最大值,
,(0<m<8);(3)当m=4时,S有最大值,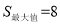 .此时,点E的坐标为(—2,0), △BCE是等腰三角形.
.此时,点E的坐标为(—2,0), △BCE是等腰三角形.
【解析】
试题分析:(1)先根据线段OB、OC的长,得到点B、C两点坐标,根据抛物线的对称性可得点A坐标;把A、B、C三点代入二次函数解析式就能求得二次函数解析式;
(2)利用A、B、C三点坐标得出AB,CO的长,即可得出△ABC的面积;易得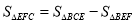 ,只需利用平行得到三角形相似,求得EF长,进而利用相等角的正弦值求得△BEF中BE边上的高;
,只需利用平行得到三角形相似,求得EF长,进而利用相等角的正弦值求得△BEF中BE边上的高;
(3)利用二次函数求出最值,进而求得点E坐标.OC垂直平分BE,那么EC=BC,所求的三角形是等腰三角形.
试题解析:(1)∵点B在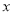 轴的正半轴上,点C在
轴的正半轴上,点C在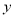 轴的正半轴上,OB=2,OC=8,∴点B的坐标为(2,0),点C的坐标为(0,8). 又∵抛物线
轴的正半轴上,OB=2,OC=8,∴点B的坐标为(2,0),点C的坐标为(0,8). 又∵抛物线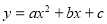 的对称轴是直线
的对称轴是直线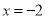 ,∴由抛物线的对称性可得点A的坐标为(-6,0).∵点C(0,8)在抛物线
,∴由抛物线的对称性可得点A的坐标为(-6,0).∵点C(0,8)在抛物线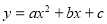 的图象上,∴c =8,将A(-6,0)、B(2,0)分别代入
的图象上,∴c =8,将A(-6,0)、B(2,0)分别代入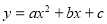 ,得:
,得: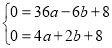 ,解得:
,解得: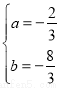 ,∴所求抛物线的表达式为
,∴所求抛物线的表达式为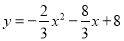 ;
;
(2)依题意,AE=m,则BE=8-m, ∵OA=6,OC=8,由勾股定理得AC=10,∵EF∥AC,∴△BEF∽△BAC.∴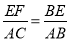 ,即
,即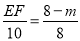 ,∴EF=
,∴EF=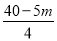 .过点F作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB=
.过点F作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB= .∴
.∴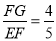 .∴FG=
.∴FG=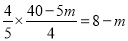 ,
,
∴S=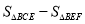 =
=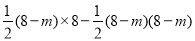 =
=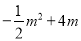 ,自变量m的取值范围是0<m<8;
,自变量m的取值范围是0<m<8;
(3)存在.理由如下:
∵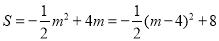 且
且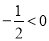 ,∴当m=4时,S有最大值,
,∴当m=4时,S有最大值,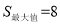 ,
,
∵m=4,∴点E的坐标为(﹣2,0),∴△BCE为等腰三角形.
考点:二次函数综合题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:填空题
科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如表:

科学家经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为_______℃.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省耒阳市九年级上学期期末考试数学试卷(解析版) 题型:选择题
要使式子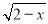 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A.x>0 B.x≥-2 C.x≥2 D.x≤2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省五常市九年级上学期12月阶段性测试数学试卷(解析版) 题型:填空题
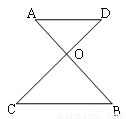
如图,线段AB、CD相交于O,AD∥BC,AO=4,CO=8,OD=3,则OB= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省五常市九年级上学期12月阶段性测试数学试卷(解析版) 题型:选择题
如图,在△ABC中,D为AC边上一点,若∠DBC=∠A,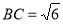 ,AC=3,则CD长为( )
,AC=3,则CD长为( )
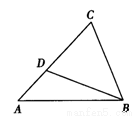
A.1 B.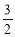 C.2 D.
C.2 D.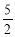
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省郑州市九年级第一次质量预测数学试卷(解析版) 题型:解答题
(9分)如图1,小颖将一组平行的纸条折叠,点A、B分别落在在A′,B′处,线段FB′与AD交于点M.

(1)试判断△MEF的形状,并证明你的结论;
(2)如图②,将纸条的另一部分CFMD沿MN折叠,点C,D分别落在C′,D′处,且使MD′经过点F,试判断四边形MNFE的形状,并证明你的结论;
(3)当∠BFE=_____度时,四边形MNFE是菱形.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省石家庄市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是AB上的任意一点,过点C的切线分别交PA、PB于点D、E.若PA=4,求△PED的周长.
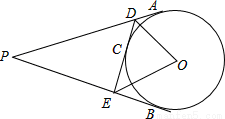
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com