Question

14．如图，∠BAC=40°，射线AB，AC分别交直角三角板DEF的两条直角边DE，DF于点B，C，连结BC．
（1）如图1，当点D在∠BAC内部时，求∠ABD+∠ACD的度数；
（2）如图2，当点D在∠BAC外部时，求∠ACD-∠ABD的度数．

Answer 1

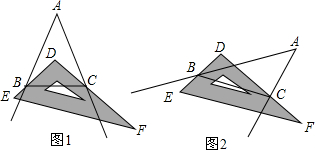
分析 （1）本题考查的是三角形内角和定理．已知∠BAC=40°易求∠ABC+∠ACB的度数．又因为∠D为90°，所以易求∠DBC+∠DCB，相减即可求出∠ABD+∠ACD；
（2）根据∠D+∠DBA=∠A+∠ACD，进而得出∠ACD-∠DBA的度数．

解答 解：（1）∵∠BAC=40°，
∴∠ABC+∠ACB=140°，
∵∠D=90°，
∴∠DBC+∠DCB=90°，
∴∠DBA+∠DCA=140°-90°=50°；
（2）∵∠D+∠DBA=∠A+∠ACD，∠D=90°，
∴90°+∠DBA=40°+∠ACD，
∴∠ACD-∠DBA=50°．

点评 考查了三角形内角和定理，此题注意运用整体法计算．关键是求出∠ABC+∠ACB．