练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】要反映我市某一周每天的最高气温的变化趋势，宜采用（ ）
    A.扇形统计图
    B.条形统计图
    C.折线统计图
    D.频数分布统计图

    【答案】C
    【解析】根据题意，要求直观反映我市一周内每天的最高气温的变化情况，结合统计图各自的特点，应选择折线统计图．故选：C．
    根据统计图的特点进行扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；折线统计图表示的是事物的变化情况；条形统计图能清楚地表示出每个项目的具体数目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：

    鸭的质量/千克

    0.5

    1

    1.5

    2

    2.5

    3

    3.5

    4

    烤制时间/分

    40

    60

    80

    100

    120

    140

    160

    180

    设鸭的质量为x千克，烤制时间为t，估计当x=3.2千克时，t的值为（　　）

    A．140 B．138 C．148 D．160

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一个多项式与3x2+9x+2的和等于3x2+4x-3，则此多项式是。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，a、b、c在数轴上的位置如图．

    （1）填空：a、b之间的距离为；b、c之间的距离为；a、c之间的距离为 ．
    （2）化简：|a+1|﹣|c﹣b|+|b﹣1|．
    （3）若a+b+c=0，且b与﹣1的距离和c与﹣1的距离相等，求﹣a2+2b﹣c﹣（a﹣4c﹣b）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

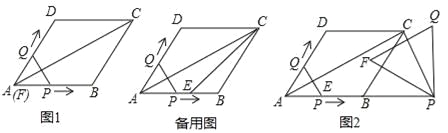
    【题目】已知：如图1，菱形ABCD的边长为6，∠DAB=60°，点E是AB的中点，连接AC、EC．点Q从点A出发，沿折线A﹣D﹣C运动，同时点P从点A出发，沿射线AB运动，P、Q的速度均为每秒1个单位长度；以PQ为边在PQ的左侧作等边△PQF，△PQF与△AEC重叠部分的面积为S，当点Q运动到点C时P、Q同时停止运动，设运动的时间为t．

    （1）当等边△PQF的边PQ恰好经过点D时，求运动时间t的值；当等边△PQF的边QF 恰好经过点E时，求运动时间t的值；

    （2）在整个运动过程中，请求出S与t之间的函数关系式和相应的自变量t的取值范围；

    （3）如图2，当点Q到达C点时，将等边△PQF绕点P旋转α°（0＜α＜360），直线PF分别与直线AC、直线CD交于点M、N．是否存在这样的α，使△CMN为等腰三角形？若存在，请直接写出此时线段CM的长度；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根．

    （1）求m的取值范围；

    （2）若m为负整数，求此时方程的根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有理数a、b、c的大小关系为：c＜b＜0＜a，则下面的判断正确的是（ ）
    A.abc＜0
    B.a﹣b＞0
    C.
    D.c﹣a＞0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各对数中，相等的是（　　）

    A. ﹣32和﹣23 B. （﹣3）2和（﹣2）3

    C. ﹣32和（﹣3）2 D. ﹣23和（﹣2）3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB=90°，BC=6，AB=10．点Q与点B在AC的同侧，且AQ⊥AC．

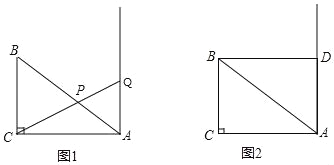
    （1）如图1，点Q不与点A重合，连结CQ交AB于点P．设AQ=x，AP=y，求y关于x的函数解析式，并写出自变量x的取值范围；

    （2）是否存在点Q，使△PAQ与△ABC相似，若存在，求AQ的长；若不存在，请说明理由；

    （3）如图2，过点B作BD⊥AQ，垂足为D．将以点Q为圆心，QD为半径的圆记为⊙Q．若点C到⊙Q上点的距离的最小值为8，求⊙Q的半径．

    查看答案和解析>>

    同步练习册答案