
 如图,在半径为1的⊙O中,AB是弦,OM是弦心距,求OM+AB的最大值.
如图,在半径为1的⊙O中,AB是弦,OM是弦心距,求OM+AB的最大值. 分析 设AM=x,根据垂径定理得到AB=2x,根据勾股定理列出关于x的方程,利用一元二次方程根的判别式解答即可.
解答 解:设AM=x,
∵OM是弦心距,
∴AB=2x,
在Rt△AOM中,OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=$\sqrt{1-{x}^{2}}$,
设OM+AB=a,即$\sqrt{1-{x}^{2}}$+2x=a,
$\sqrt{1-{x}^{2}}$=a-2x,
1-x2=a2-4ax+4x2,
5x2-4ax+(a2-1)=0,
△=(-4a)2-4×5×(a2-1)≥0,即a2≤5,
解得,-$\sqrt{5}$≤a≤$\sqrt{5}$,
则a的最大值为$\sqrt{5}$,即OM+AB的最大值为$\sqrt{5}$.
点评 本题考查的是垂径定理的应用以及一元二次方程根的判别式的应用,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
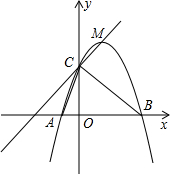 如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(-1,0),点C(0,5),点D(1,8)都在抛物线上,M为抛物线的顶点.
如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(-1,0),点C(0,5),点D(1,8)都在抛物线上,M为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
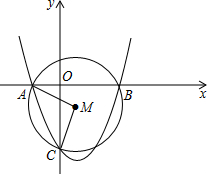 如图,二次函数y=x2-2x-3的图象经过(a,0),B(b,0),C(0,c)三点,(a<b)
如图,二次函数y=x2-2x-3的图象经过(a,0),B(b,0),C(0,c)三点,(a<b)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
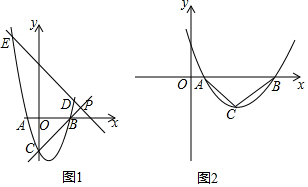
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
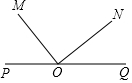 如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )
如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )| A. | ∠MOQ | B. | ∠MON | C. | ∠NOQ | D. | ∠PON |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
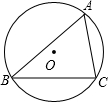 如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R.
如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com