
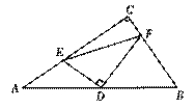
【题目】如图,已知△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.
求证:AE2+BF2=EF2.
科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上: .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别![]() a、
a、![]() a、
a、![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
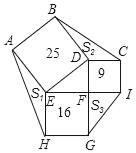
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
(1)先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为 , 若A为随机事件,则m的取值为;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
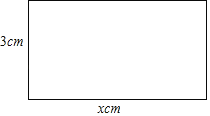
【题目】如图,已知长方形相邻两边的长分别是xcm和3cm,设长方形的面积为ycm2.
(1)试写出长方形的面积y与x之间的关系式;
(2)利用(1)中的关系式,求当x=5cm时长方形的面积;
(3)当x的值由4cm变化到12cm时,长方形的面积由 cm2变化到 cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com