Question

【题目】在平行四边形ABCD中，AB=10，∠ABC=60°，以AB为直径作⊙O，边CD切⊙O于点E．

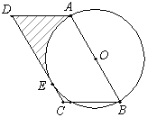
(1)圆心O到CD的距离是______；

(2)求由弧AE、线段AD、DE所围成的阴影部分的面积．（结果保留π和根号）

Answer 1

【答案】(1)、5；(2)、25+-.

【解析】

试题分析：(1)、连接OE，根据切线可得OE⊥CD，根据AB求出OE的长度，即圆心到CD的距离；(2)、根据平行四边形得出∠C=120°，∠BOE=90°，作EF∥CB，根据Rt△OEF求出OF的长度，然后得出EC和DE长度，从而求出梯形OADE的面积和扇形OAE的面积，从而得出阴影部分的面积.

试题解析：(1)、连接OE．

∵边CD切⊙O于点E．∴OE⊥CD 则OE就是圆心O到CD的距离，则圆心O到CD的距离是×AB=5．

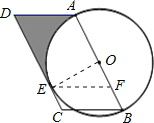
（2）∵四边形ABCD是平行四边形． ∴∠C=∠DAB=180°-∠ABC=120°，

∴∠BOE=360°-90°-60°-120°=90°， ∴∠AOE=90°，

作EF∥CB，∴∠OFE=∠ABC=60°， 在直角三角形OEF中，OE=5，

∴OF=OEtan30°=．EC=BF=5-． 则DE=10-5+=5+，

则直角梯形OADE的面积是：（OA+DE）×OE=（5+5+）×5=25+．

扇形OAE的面积是：． 则阴影部分的面积是：25+-．