
如图,,四边形OABC为直角梯形,点A、B、C的坐标分别是(2,6),(8,6),(8,0).动点F、D分别从O、B同时出发,以每秒1个单位速度.其中点F沿着OC向终点C运动,点D沿着BA方向向终点A运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点D做DE AB,交OB于E,连接EF,已知动点运动了x秒.
AB,交OB于E,连接EF,已知动点运动了x秒.

1.x的取值范围多少?
2.E 点坐标是 ;(用含代数式表示)
3.试求△OFE面积最大值,并求此时x的值.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 21、已知:如图,在Rt△OAB中,∠OAB=90°,OA=AB=6cm,将△OAB绕点O沿逆时针方向旋转90°得到Rt△OA1B1
21、已知:如图,在Rt△OAB中,∠OAB=90°,OA=AB=6cm,将△OAB绕点O沿逆时针方向旋转90°得到Rt△OA1B1查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.
(2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.| EF |
| JI |
| DE |
| HI |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
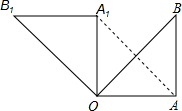 到△OA1B1.
到△OA1B1.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,△OAB绕点O旋转l80°得到△OCD,连接AD,BC,得到四边形ABCD.
如图所示,△OAB绕点O旋转l80°得到△OCD,连接AD,BC,得到四边形ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com