


分析 (1)根据水面与水平面平行可以得到CQ与BE平行,利用勾股定理即可求得BQ的长;
(2)液体正好是一个以△BCQ是底面的直棱柱,据此即可求得液体的体积;
(3)根据液体体积不变,当0°≤α≤37°时,列方程$\frac{1}{2}$(x+y)×4×4=24和当37°<α≤53°时,列方程$\frac{1}{2}$×y×(4-x)×4=24,求解即可.
解答 解:(1)∵液体的形状为直三棱柱,
∴CQ∥BE,
根据勾股定理得.BQ=$\sqrt{{5}^{2}-{4}^{2}}$=3;
在Rt△BCQ中,tan∠BCQ=$\frac{3}{4}$,
∴α=∠BCQ=37°.
故答案为CQ∥BE,3,37°.
(2)V液=$\frac{1}{2}$×3×4×4=24(dm3);
(3)当容器向左旋转时,0°≤α≤37°,
∵液体体积不变,
∴$\frac{1}{2}$(x+y)×4×4=24,
∴y=-x+3.
当容器向右旋转时,37°<α≤53°,
∵液体体积不变,
∴$\frac{1}{2}$×y×(4-x)×4=24,
∴y=$\frac{12}{4-x}$;
当液面恰好到达容器口沿,即点Q与点B′重合时,如图5,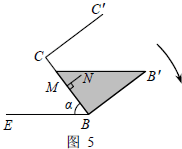
∵BB′=4,且$\frac{1}{2}$PB•BB′×4=24,
∴PB=3,
∴tan∠PB′B=$\frac{3}{4}$,
∴∠PB′B=37°.
∴α=∠B′PB=53°.
此时37°≤α≤53°;
点评 本题是几何变换综合题,主要考查了四边形的体积计算以及三视图的认识,正确理解棱柱的体积的计算是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
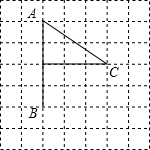 如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )| A. | (2,3) | B. | (1,3) | C. | (3,1) | D. | (3,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -7,2 | B. | -$\frac{1}{7}$,2 | C. | -$\frac{1}{7}$,3 | D. | $\frac{1}{7}$,3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com