
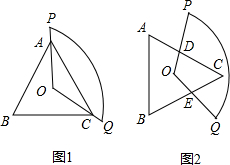

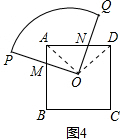
 解:(1)①a;(1分)
解:(1)①a;(1分)| 360° |
| n |
| 360° |
| n |


科目:初中数学 来源: 题型:
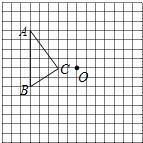 17、在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出△ABC绕点O逆时针旋转90°后的△A′B′C′.
17、在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出△ABC绕点O逆时针旋转90°后的△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:
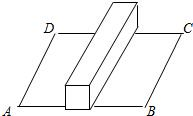 在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处,到达C处需要走的最短路程是
在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处,到达C处需要走的最短路程是查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
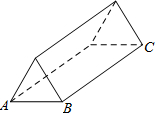 一个蔬菜大棚(四周都是塑料薄膜)的形状如图.
一个蔬菜大棚(四周都是塑料薄膜)的形状如图.查看答案和解析>>
科目:初中数学 来源: 题型:
 在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处,到达C处需要走的最短路程是
在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处,到达C处需要走的最短路程是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com