解:(1)(方法一)由题意:设抛物线的解析式为y=a(x+1)(x-3)
∴y=ax
2-2ax-3a=a(x-1)
2-4a,
∴点C(0,-3a),D(1,-4a),
(方法二)由题意:
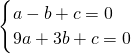
,
解得
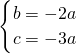
.
∴y=ax
2-2ax-3a(下同方法一);
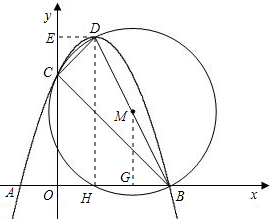
(2)(方法一)过点D作DE⊥y轴于点E,易证△DEC∽△COB
∴
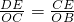
∴
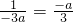
∴a
2=1.
∵a<0,
∴a=-1.
故抛物线的解析式为:y=-x
2+2x+3.
(方法二)过点D作DE⊥y轴于点E,过M作MG⊥x轴于点G,
设⊙M交x轴于另一点H,交y轴于另一点F,可先证四边形OHDE为矩形,则OH=DE=1,再证OF=CE=-a,
由OH•OB=OF•OC得:(-a)(-3a)=1×3,
∴a
2=1;(下同法一)
(3)符合条件的点P存在,共3个
①若∠BPD=90°,P点与C点重合,则P
1(0,3)(P
1表示第一个P点,下同)
②若∠DBP=90°,过点P
2作P
2R⊥x轴于点R,
设点P
2(p,-p
2+2p+3)
由△BP
2R∽△DBH得,
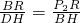
,
即
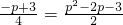
,
解得
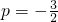
或p=3(舍去)
故
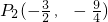
③若∠BDP=90°,设DP
3的延长线交y轴于点N,可证△EDN∽△HDB,
求得EN=

,
∴N(0,

).
求得DN的解析式为
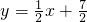
,
求抛物线与直线DN的交点得P
3(
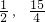
),
综上所述:符合条件的点P为(0,3)、
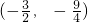
、(
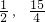
).
分析:(1)点A(-1,0)和B(3,0)一定关于抛物线的对称轴对称,因而函数的对称轴是x=1,把x=1代入抛物线的解析式就可以求出D的坐标;
(2)过点D作DE⊥y轴于点E,易证△DEC∽△COB,根据相似三角形的对应边的比相等就可以求出a的值.从而求出抛物线的解析式;
(3)本题应分∠BPD=90°,∠DBP=90°,∠BDP=90°三种情况进行讨论.第一种情况P就是满足条件的点.
第二种情况中,过点P
2作P
2R⊥x轴于点R,由△BP
2R∽△DBH就可以求出.
第三种情况,设DP
3的延长线交y轴于点N,可证△EDN∽△HDB,求出直线DN的解析式,就可以求抛物线与直线DN的交点.
点评:本题是二次函数与圆以及相似三角形相结合的题目,难度较大,利用数形结合有利于对题目的理解.

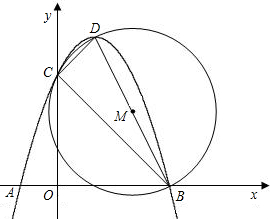 于点C,顶点为D,以BD为直径的⊙M恰好过点C.
于点C,顶点为D,以BD为直径的⊙M恰好过点C.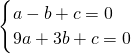 ,
,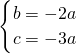 .
.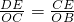 ∴
∴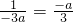

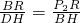 ,
,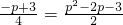 ,
,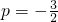 或p=3(舍去)
或p=3(舍去)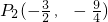
 ,
, ).
).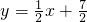 ,
,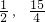 ),
),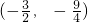 、(
、(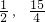 ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.