
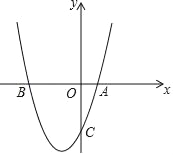
【题目】如图,抛物线y=x2﹣2mx+3m与x轴交于A、B两点,与y轴交于点C(0,﹣3)
(1)求该抛物线的解析式;
(2)点D为该抛物线上的一点、且在第二象限内,连接AC,若∠DAB=∠ACO,求点D的坐标;
(3)若点E为线段OC上一动点,试求2AE+![]() EC的最小值.
EC的最小值.
【答案】(1)y=x2+2x﹣3;(2)点D的坐标为(﹣![]() ,
,![]() );(3)4
);(3)4![]() .
.
【解析】
(1)把点C的坐标代入抛物线求出m,即可求出解析式;
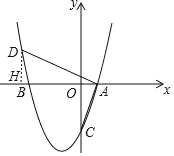
(2)过D点作x轴的垂线,交x轴于点H,点D的坐标为(n,n 2+2 n﹣3),易知∠DAB =∠ACO ,利用tan∠DAB=tan∠ACO即可求得n的值,即可求出D点坐标;
(3)根据B,C坐标求出直线BC的解析式为y=-x-3,故∠BCO=45°,则EF=![]() EC,AE+
EC,AE+![]() EC=AE+EF,故当A、E、F三点共线时,AE+
EC=AE+EF,故当A、E、F三点共线时,AE+![]() EC最小,即2AE+
EC最小,即2AE+![]() EC最小,
EC最小,
根据BC⊥AF可设直线AF的表达式为:y=x+b,代入A点即可求出直线AF,令x=0,可求出E点坐标,即可求出此时2AE+![]() EC的值.
EC的值.
解:(1)把点C的坐标代入抛物线表达式得:9+6m+3m=0,
解得:m=﹣1,
故该抛物线的解析式为:y=x2+2x﹣3;
(2)过D点作x轴的垂线,交x轴于点H,过点E作EF⊥BC,交BC于点F,
令y=0,求得A(1,0),B(-3,0).
设:点D的坐标为(n,n 2+2n﹣3),
∵∠DAB=∠ACO,
∴tan∠DAB=tan∠ACO,
即:![]() =
=![]() ,
,![]() =
=![]() ,
,
解得:![]() =
=![]() 或1(舍去m=1),
或1(舍去m=1),
故点D的坐标为(![]() ,
,![]() );
);
(3)根据B,C坐标求出直线BC的解析式为y=-x-3,
过点E作EF⊥BC,交BC于点F,
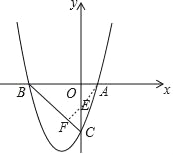
则EF=![]() EC,AE+
EC,AE+![]() EC=AE+EF,
EC=AE+EF,
∴当A、E、F三点共线时,AE+![]() EC最小,即2AE+
EC最小,即2AE+![]() EC最小,
EC最小,
设:直线AF的表达式为:y=x+b,
将点A坐标(1,0)代入上式,1+b=0,则b=﹣1,
则直线AE的表达式为:y=x﹣1,则点E的坐标为(0,﹣1),
则EC=3﹣1=2,AE=![]()
2AE+![]() EC=2
EC=2![]() +2
+2![]() =4
=4![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )
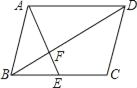
A. BF=![]() DFB. S△AFD=2S△EFBC. 四边形AECD是等腰梯形D. ∠AEB=∠ADC
DFB. S△AFD=2S△EFBC. 四边形AECD是等腰梯形D. ∠AEB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
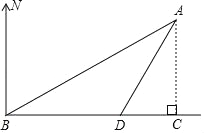
【题目】如图,海中有一小岛A,它周围8海里内有暗礁,渔船由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.
(1)求∠BAD的度数;
(2)如果渔船不改变航线继续向东航行,有没有触礁的危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() (a为常数)的图象与y轴相交于点A,与函数
(a为常数)的图象与y轴相交于点A,与函数![]() (x>0)的图象相交于点B(m,1).
(x>0)的图象相交于点B(m,1).
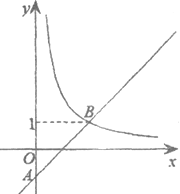
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(x1,y1)、B(x2,y2)都在某函数图象上,且当x1<x2<0时,y1>y2,则此函数一定不是( )
A. ![]() B. y=﹣2x+1 C. y=x2﹣1 D.
B. y=﹣2x+1 C. y=x2﹣1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
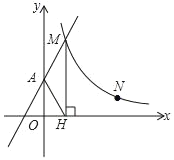
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求H点的坐标及k的值;
(2)点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;
(3)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
(x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
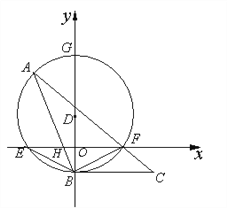
【题目】如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在![]() 上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
(1)判断直线BC与⊙D的位置关系,并说明理由;
(2)求证:BE2=BH·AB;
(3) 若点E坐标为(-4,0),点B的坐标为(0,-2),AB=8,求F与A两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
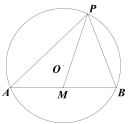
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).


图① 图② 图③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com