
 如图,AB=CD,AD=BC,∠1=50°,∠2=24°,则∠B的度数是106度.
如图,AB=CD,AD=BC,∠1=50°,∠2=24°,则∠B的度数是106度.  同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们把过三角形的一个顶点且能将这个三角形分割成两个等腰三角形的线段称为该三角形的“等腰线段”.
我们把过三角形的一个顶点且能将这个三角形分割成两个等腰三角形的线段称为该三角形的“等腰线段”.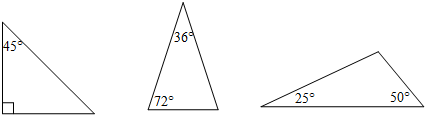

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com