练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．如图，一次函数y=x与二次函数y=ax2+bx+c图象相交于A、B两点，则函数y=ax2+（b-1）x+c的图象可能是（　　）
    A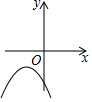．B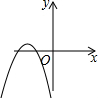．C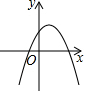．D．

    分析 由直线y=x与抛物线y=ax2+bx+c有两个交点，且两交点的横坐标均为负数可知：方程ax2+bx+c=x，即ax2+（b-1）x+c=0有两个同为异号的实数根，根据二次函数的图象与一元二次方程的根之间的关系即可得．

    解答 解：由图象知直线y=x与抛物线y=ax2+bx+c有两个交点，且两交点的横坐标均为负数，
    ∴方程ax2+bx+c=x，即ax2+（b-1）x+c=0有两个同为异号的实数根，
    ∴函数y=ax2+（b-1）x+c的图象与x轴的负半轴有两个交点，
    故选：B．

    点评 本题主要考查二次函数的图象与一元二次方程的根之间的关系，由题目已知图象得出方程ax2+bx+c=x，即ax2+（b-1）x+c=0有两个同为异号的实数根是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．已知，△ABC在平面直角坐标系中的位置如图所示．
    （1）把△ABC向下平移2个单位长度得到△A1B1C1，请画出△A1B1C1；
    （2）请画出△A1B1C1关于y轴对称的△A2B2C2，并写出A2的坐标； 
    （3）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

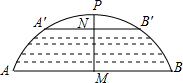    19．如图所示，有一座拱桥圆弧形，它的跨度AB为60米，拱高PM为18米，当洪水泛滥到跨度只有30米时，就要采取紧急措施，若拱顶离水面只有4米，即PN=4米时，是否采取紧急措施？（$\sqrt{2}$=1.414）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

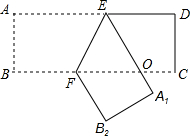    16．如图，把一张长方形纸片ABCD沿EF折叠后，点A、B分别落在A1、B2的位置上，A1E与BC交于点O，若∠EFO=60°，则∠AEA1=120°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知，圆的直径为13cm，直线到圆心的距离为d，当d=8cm时，直线与圆相离，当d=6.5cm时，直线与圆相切；当d小于6.5cm时，直线与圆相交．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．小芳的房间有高为3m的玻璃窗，她站在室内离窗户4m的地方向外看，她能看到窗前面一楼房的高度范围是18m（楼房之间的距离为20m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．若分式$\frac{-6}{x+5}$的值是整数，则整数x的值是1或-11或4或-6或3或-7或2或-8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，在△ABC中，∠A=30°，∠B=45°，AC=2$\sqrt{3}$，则CB的长为$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．某公司2007年的利润是a万元，计划以后每年在前一年的基础上增长m%，则2010年的利润是（　　）
    A．a（1+m%）2B．a（1+m%）3C．a（1+m%）4D．（a+m%）3

    查看答案和解析>>

    同步练习册答案