练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （1）如图1，阴影部分是由5个小正方形组成的一个直角图形，请用两种方法分别在下图方格内涂黑两个小正方形，使它们成为轴对称图形．如图2是4×4正方形网格，请在其中选取一个白色的单位正方形并涂黑，使图2中阴影部分是一个中心对称图形．
    （2）如图3所示，快下降到地面的某伞兵在灯光下的影子为AB．试确定灯源P的位置，并画出竖立在地面上木桩的影子EF．（保留作图痕迹，不要求写作法）

    【答案】分析：（1）利用轴对称图形与中心对称图形的定义即可画出；
    （2）经过A，B两点的光线的交点就是光源P的位置，过P与作出经过木桩顶端的光线与地面的交点，到木桩底部的部分就是阴影．
    解答：解：（1）

    （2）

    点评：本题考查了轴对称图形与中心对称图形的定义，以及视图的内容，正确确定光源P的位置是解决（2）的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    下列图①、②、③中的阴影部分分别是以直角三角形的三边为边长所作的正多边形；图④中的阴影部分分别是以直角三角形的三边为直径所作的半圆．根据勾股定理可知：分别以直角三角形的两条直角边为边长的正方形面积之和等于以斜边为边长的正方形的面积（如图②）
    （1）类似的结论，对于图②的结论，对于图①、③、④是否成立？如果成立，请选择其中一个图形进行证明．
    （2）根据（1）的结论，你能提出一般性的结论吗？写出你的结论并给予证明．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，一直角三角形三边长分别为6，8，10，且分别是三个半圆的直径，求阴影部面积（π取3）．

    查看答案和解析>>

    科目：初中数学 来源：中学教材全解　七年级数学下　(北京师大版) 北京师大版 题型：044

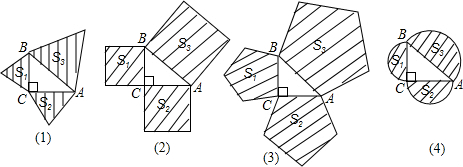
    “抛阶砖”是游戏场的典型游戏之一．如图(1)，参与者只需将手上的“金币”抛落身边若干距离的阶砖平面上，抛出的硬币刚巧落在任何一个阶砖的范围内(不与阶砖相连的线重叠)，便可获奖．要注意“金币”与阶砖的相对大小将会决定成功抛中阶砖的机会．由于阶砖是正方形，可设每边长度为a，金币的直径为d．若“金币”成功落在阶砖上，它的圆心必位于图(2)的阴影部分内，即“成功”部分是边长为(a－d)的正方形．

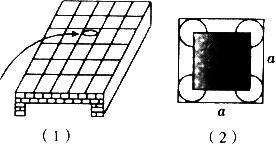
    (1)计算“金币”抛落在阶砖范围内的概率(用含a、d的式子表示，0＜d＜a)；

    (2)通过配搭“金币”与阶砖之间的大小的设计，做这个“抛阶砖”的游戏，并作好记录，你发现什么规律？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    下列图①、②、③中的阴影部分分别是以直角三角形的三边为边长所作的正多边形；图④中的阴影部分分别是以直角三角形的三边为直径所作的半圆．根据勾股定理可知：分别以直角三角形的两条直角边为边长的正方形面积之和等于以斜边为边长的正方形的面积（如图②）
    （1）类似的结论，对于图②的结论，对于图①、③、④是否成立？如果成立，请选择其中一个图形进行证明．
    （2）根据（1）的结论，你能提出一般性的结论吗？写出你的结论并给予证明．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    下列图①、②、③中的阴影部分分别是以直角三角形的三边为边长所作的正多边形；图④中的阴影部分分别是以直角三角形的三边为直径所作的半圆．根据勾股定理可知：分别以直角三角形的两条直角边为边长的正方形面积之和等于以斜边为边长的正方形的面积（如图②）
    （1）类似的结论，对于图②的结论，对于图①、③、④是否成立？如果成立，请选择其中一个图形进行证明．
    （2）根据（1）的结论，你能提出一般性的结论吗？写出你的结论并给予证明．

    精英家教网

    查看答案和解析>>

    同步练习册答案