
 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.分析 (1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是⊙O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)连接AE,利用已知条件分别求出BC,CE的长,由BE=BC-CE计算即可.
解答 (1)证明:连结BD.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠DAB+∠DBA=90°.
∵AB=AC,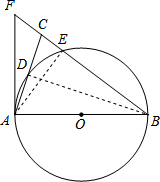
∴2∠ABD=∠ABC,AD=$\frac{1}{2}$AC.
∵AF为⊙O的切线,
∴∠FAB=90°.
∴∠FAC+∠CAB=90°.
∴∠FAC=∠ABD.
∴∠ABC=2∠CAF.
(2)解:连接AE.
∴∠AEB=∠AEC=90°.
∵$sin∠CAF=\frac{{\sqrt{10}}}{10}\;,\;\;∠ABD=∠CAF\;=∠CBD=∠CAE$,
∴$sin∠ABD=sin∠CAF=\frac{{\sqrt{10}}}{10}$.
∵$∠ABD=90°\;,\;\;AC=2\sqrt{10}$,
∴$AD=\sqrt{10}$,$AB=\frac{AD}{sin∠ABD}=10$.
∵$∠AEC=90°\;,\;\;AC=2\sqrt{10}$,
∴CE=AC•sin∠CAE=2.
∴BE=BC-CE=10-2=8.
点评 此题考查了切线的性质、三角函数以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 | a | b |
| a | a2 | ab |
| -b | -ab | -b2 |
 | x2 | -2x | 4 |
| x | x3 | -2x2 | 4x |
| +2 | 2x2 | -4x | 8 |
 | m2 | -3m | 9 |
| m | m3 | -3m2 | 9m |
| +3 | 3m2 | -9m | 27 |
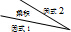 | |||
| △ | △3 | ||
| ○ | ○3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲、乙两车分别从A,B两地同时相向匀速行驶.当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则B,C两地相距600千米.
甲、乙两车分别从A,B两地同时相向匀速行驶.当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则B,C两地相距600千米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com