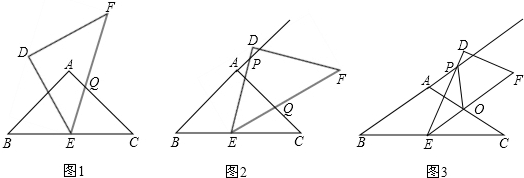
（1）如图1，把两块全等的含45°的直角三角板ABC和DEF叠放在一起，使三角板DEF的锐角顶点E与三角板ABC的斜边中点重合．可知：△BPE∽△CEQ （不需说理）
（2）如图2，在（1）的条件下，把三角板ABC固定不动，让三角板DEF绕点E旋转，让三角板两边分别与线段BA的延长线、边AC的相交于点P、Q，连接PQ．
①若BC=4，设BP=x，CQ=y，则y与x的函数关系式为
；
②写出图中能用字母表示的相似三角形
；
③试判断∠BPE与∠EPQ的大小关系？并说明理由．
（3）如图3，在（2）的条件下，将三角板ABC改为等腰三角形，且AB=AC，三角板DEF改为一般三角形，其它条件不变，要使（2）中的结论③成立，猜想∠BAC与∠DEF关系为
．（将结论直接填在横线上）
（4）如图3，在（1）的条件下，将三角板ABC改为等腰三角形，且∠BAC=120°，AB=AC，三角板DEF改为∠DEF=30°直角三角形，把三角板ABC固定不动，让三角板DEF绕点E旋转，让三角板两边分别与线段BA的延长线、边AC的相交于点P、Q，连接PQ．若S
△PEQ=2，PQ=2，求点C到AB的距离．
优百分课时互动系列答案
开心蛙状元作业系列答案
在△ABC中，∠C=90°，AC=AE，DE⊥AB于E点，∠CDA=55°，则∠BDE=