练习册

  • 练习册
  • 试题
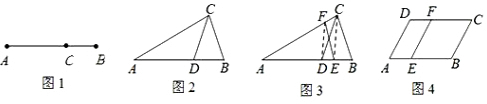
    精英家教网 > 初中数学 > 题目详情

    三角形的一条中线是否将这个三角形分成面积相等的两个三角形？为什么？

    答案：略
    解析：

    能．根据等底等高的两个三角形的面积相等的结论．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图1，点C将线段AB分成两部分，如果
    AC
    AB
    =
    BC
    AC
    ，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果
    S1
    S
    =
    S2
    S1
    ，那么称直线l为该图形的黄金分割线．
    （1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？
    （2）请你说明：三角形的中线是否也是该三角形的黄金分割线？
    （3）研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF（如图3），则直线EF也是△ABC的黄金分割线．请你说明理由．
    （4）如图4，点E是平行四边形ABCD的边AB的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是平行四边形ABCD的黄金分割线．请你画一条平行四边形ABCD的黄金分割线，使它不经过平行四边形ABCD各边黄金分割点．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    24、如图，已知：AD是△ABC中BC边的中线，则S△ABD=S△ACD，依据是
    等底等高的三角形面积相等

    规定；若一条直线l把一个图形分成面积相等的两个图形，则称这样的直线l叫做这个图形的等积直线．根据此定义，在图1中易知直线为△ABC的等积直线．
    （1）如图2，在矩形ABCD中，直线l经过AD，BC边的中点M、N，请你判断直线l是否为该矩形的等积直线
    是
    （填“是”或“否”）．在图2中再画出一条该矩形的等积直线．（不必写作法）
    （2）如图3，在梯形ABCD中，直线l经过上下底AD、BC边的中点M、N，请你判断直线l是否为该梯形的等积直线
    是
    （填“是”或“否”）．
    （3）在图3中，过M、N的中点O任作一条直线PQ分别交AD，BC于点P、Q，如图4所示，猜想PQ是否为该梯形的等积直线？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

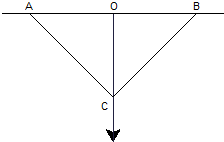    28、汶川大地震过后，某中学的同学用下面的方法检测教室的房梁是否水平：在等腰直角三角尺斜边中点拴一条线绳，线绳的另一端挂一个铅锤，把这块三角尺的斜边贴在房梁上，结果线绳经过三角尺的直角顶点，同学们确信房梁是水平的，理由是
    等腰三角形的底边上的中线、底边上的高重合
    ．

    查看答案和解析>>

    科目：初中数学 来源：新课标教材导学　　数学七年级(第二学期) 题型：044

    三角形的一条中线是否将这个三角形分成面积相等的两个三角形？为什么？

    查看答案和解析>>

    同步练习册答案