
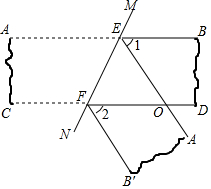
 如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.分析 (1)根据平行线的性质得到∠MEB=∠NFD,∠NEA′=∠MFB′,根据角的和差即可得到结论;
(2)由折叠知,∠B′FN=$\frac{180°-∠2}{2}$=70°,根据平行线的性质得到∠A′EN=∠B′FN=70°,即可得到结论.
解答 解:(1)∵AB∥CD,∴∠MEB=∠MFD,
∵A′E∥B′F,
∴∠MEA′=∠MFB′,
∴∠MEA′-∠MEB=∠MFB′-∠MFD,
即∠1=∠2;
(2)由折叠知,∠B′FN=$\frac{180°-∠2}{2}$=70°,
∵A′E∥B′F,
∴∠A′EN=∠B′FN=70°,
∵∠1=∠2,
∴∠BEF=70°+40°=110°.
点评 本题考查了平行线的性质,折叠的性质,熟练掌握平行线的性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每月用水量 | 单价(元/m3) |
| 不超过8m3的部分 | 2 |
| 超出8m3,但不超出12m3的部分 | 4 |
| 超出12m3的部分 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
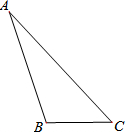 按下列要求画图并填空:
按下列要求画图并填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com