
 AB.
AB. ,
, AB.
AB. ,
, ,
,
 ,
, ,
,

科目:初中数学 来源: 题型:
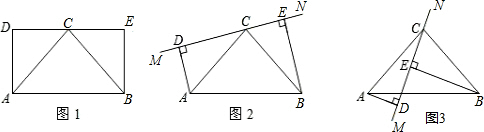
 23、已知:如图,梯形ABCD中,AD∥BC,E是BC的中点,∠BEA=∠DEA,连接AE、BD相交于点F,BD⊥CD.
23、已知:如图,梯形ABCD中,AD∥BC,E是BC的中点,∠BEA=∠DEA,连接AE、BD相交于点F,BD⊥CD.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
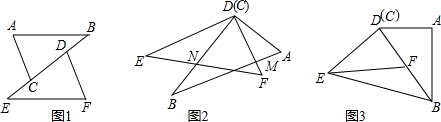
如图所示,已知:四边形ABCD中,AB=DC、AC=BD、AD≠BC,求证:四边形ABCD是等腰梯形。

证明:过点D作DE∥AB,交BC于E,则∠ABE=∠1。 ①
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB. ②
∴∠ABC=∠DCB. ③
∴∠1=∠DCB. ④
∴AB=DC=DE。 ⑤
∴四边形ABED是平行四边形。 ⑥
∴AD∥BC, ⑦
BE=AD. ⑧
又∵AD≠BC,∴BE≠BC.
∴点E、C是不同的点,DC不平行AB. ⑨
又∵AB=CD,∴四边形ABCD是等腰梯形。 ⑩
读后完成下列各小题。
(1)证明过程是否有错误?如有错在第几步上。答:______________。
(2)作DE∥AB的目的是________________________。
(3)有人认为第9步是多余的,你的看法是______________。
(4)判断四边形ABED为平行四边形的依据是______________。
(5)判断四边形ABCD是等腰梯形的依据是______________。
(6)若题设中没有AD≠BC,那么四边形ABCD一定是等腰梯形吗?你的意见是______________。
查看答案和解析>>
科目:初中数学 来源: 题型:044
阅读:下面是某同学证明一道几何题的过程.
已知:四边形ABCD中,AB=DC,AC=BD,AD≠BC
求证:四边形ABCD是等腰梯形.
证明:过D作DE∥AB交BC于E(如图所示),
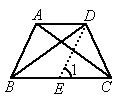
则∠ABE=∠1,①
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB,②
∴∠ABC=∠DCB,③
∴∠1=∠DCB,④
∴AB=DC=DE,⑤
∴四边形ABED是平行四边形.⑥
∴AD∥BC.⑦
BE=AD.⑧
又AD≠BC,∴BE≠BC.
∴点E,C是不同的点,DC不平行于AB.⑨
∵AB=CD,∴四边形ABCD是等腰梯形.⑩
读后填空:
(1)证明过程是否有错误?如有,错在第几步.答:__________;
(2)作DE∥AB的目的是__________;
(3)有人认为第9步是多余的,你认为是否多余?为什么?答:________;
(4)判断四边形ABED为平行四边形的依据是__________;
(5)判断四边形ABCD是等腰梯形的依据是__________;
(6)若题目中没有AD≠BC,那么四边形ABCD一定是等腰梯形吗?为什么?答_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com