
分析 (1)根据有理数的加法可以解答本题;
(2)根据有理数的乘除法可以解答本题;
(3)根据有理数的乘除法和加法可以解答本题;
(4)根据幂的乘方、有理数的乘除法和加减法可以解答本题.
解答 解:(1)(-25)+34+56+(-65)
=[(-25)+(-65)]+(34+56)
=(-90)+90
=0;
(2)(-81)÷$\frac{9}{4}$×$\frac{4}{9}$÷(-16)
=$81×\frac{4}{9}×\frac{4}{9}×\frac{1}{16}$
=1;
(3)(-5)×6+(-125)÷(-5)
=(-30)+25
=-5;
(4)-23+|-42|×(-$\frac{3}{4}$)2-27÷(-3)3
=-8+16×$\frac{9}{16}$-27÷(-27)
=-8+9+1
=2.
点评 本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
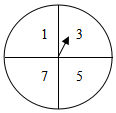 A超市在一次周年庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖机会,抽奖规则如下:将如图所示的图形转盘平均分成四个扇形,分别标上1,3,5,7四个数字,抽奖者连续转动转盘两次,当每次停止后指针所指扇形内的数为每次所得数(若指针指在分界处重转),当两次所得数字之和为2时,返现金20元,当两次所得数字之和为4时,返现金10元,当两次所得数字之和为6时,返现金5元.
A超市在一次周年庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖机会,抽奖规则如下:将如图所示的图形转盘平均分成四个扇形,分别标上1,3,5,7四个数字,抽奖者连续转动转盘两次,当每次停止后指针所指扇形内的数为每次所得数(若指针指在分界处重转),当两次所得数字之和为2时,返现金20元,当两次所得数字之和为4时,返现金10元,当两次所得数字之和为6时,返现金5元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
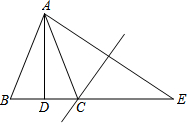 如图,等腰三角形ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则△ABC的周长等于20cm.
如图,等腰三角形ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则△ABC的周长等于20cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com