



科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 种果汁原料和
种果汁原料和 种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制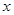 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为 元.
元. 与
与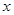 之间的函数关系式;
之间的函数关系式; 种果汁原料和17.2千克
种果汁原料和17.2千克 种果汁原料试制甲、乙两种新型饮料,右表是试验的相关数据;请你列出关于
种果汁原料试制甲、乙两种新型饮料,右表是试验的相关数据;请你列出关于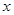 且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使
且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使 值最小,最小值是多少?
值最小,最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com