
 (2012•莱芜)某市规划局计划在一坡角为16°的斜坡AB上安装一球形雕塑,其横截面示意图如图所示.已知支架AC与斜坡AB的夹角为28°,支架BD⊥AB于点B,且AC、BD的延长线均过⊙O的圆心,AB=12m,⊙O的半径为1.5m,求雕塑最顶端到水平地面的垂直距离(结果精确到0.01m,参考数据:cos28°≈0.9,sin62°≈0.9,sin44°≈0.7,cos46°≈0.7).
(2012•莱芜)某市规划局计划在一坡角为16°的斜坡AB上安装一球形雕塑,其横截面示意图如图所示.已知支架AC与斜坡AB的夹角为28°,支架BD⊥AB于点B,且AC、BD的延长线均过⊙O的圆心,AB=12m,⊙O的半径为1.5m,求雕塑最顶端到水平地面的垂直距离(结果精确到0.01m,参考数据:cos28°≈0.9,sin62°≈0.9,sin44°≈0.7,cos46°≈0.7).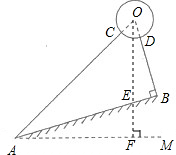 解:过点O作OF⊥AM于点F,交AB于点E,
解:过点O作OF⊥AM于点F,交AB于点E,| AB |
| AO |
| OF |
| AO |
| OF |
| 13.33 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
 哪位同学的调查方式最合理.
哪位同学的调查方式最合理.
| 类别 | 频数(人数) | 频率 |
| 武术类 | 0.25 | |
| 书画类 | 20 | 0.20 |
| 棋牌类 | 15 | b |
| 器乐类 | ||
| 合计 | a | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com