Question

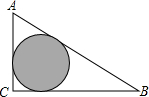
17．如图，△ABC是一块绿化带，将阴影部分修建为花圃，已知AB=15，AC=9，BC=12，阴影部分是△ABC的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为（　　）

• A． $\frac{1}{6}$
• B． $\frac{π}{6}$
• C． $\frac{π}{8}$
• D． $\frac{π}{5}$

Answer 1

分析 由AB=15，BC=12，AC=9，得到AB²=BC²+AC²，根据勾股定理的逆定理得到△ABC为直角三角形，于是得到△ABC的内切圆半径=$\frac{12+9-15}{2}$=3，求得直角三角形的面积和圆的面积，即可得到结论．

解答 解：∵AB=15，BC=12，AC=9，
∴AB²=BC²+AC²，
∴△ABC为直角三角形，
∴△ABC的内切圆半径=$\frac{12+9-15}{2}$=3，
∴S_△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×12×9=54，
S_圆=9π，
∴小鸟落在花圃上的概率=$\frac{9π}{54}$=$\frac{π}{6}$，
故选B．

点评 本题考查了几何概率，直角三角形内切圆的半径等于两直角边的和与斜边差的一半．同时也考查了勾股定理的逆定理．