
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:阅读理解
| 3 |
| 3 |
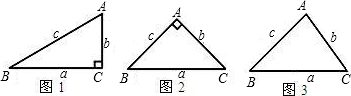 长,不必说明理由.
长,不必说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
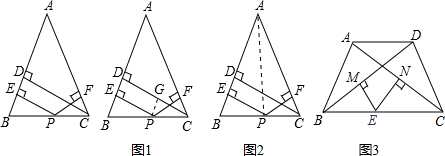
查看答案和解析>>
科目:初中数学 来源: 题型:
 小明与小亮玩游戏,他们将牌面数字分别是2,3,4的三张扑克牌充分洗匀后,背面朝上放在桌面上.规定游戏规则如下:先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再从中随机抽出一张牌,将牌面数字作为个位上的数字.如果组成的两位数恰好是2的倍数.则小明胜;如果组成的两位数恰好是3的倍数.则小亮胜.
小明与小亮玩游戏,他们将牌面数字分别是2,3,4的三张扑克牌充分洗匀后,背面朝上放在桌面上.规定游戏规则如下:先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再从中随机抽出一张牌,将牌面数字作为个位上的数字.如果组成的两位数恰好是2的倍数.则小明胜;如果组成的两位数恰好是3的倍数.则小亮胜.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com