
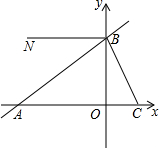
 如图,在坐标系中,直线y=-3x+6与x轴的正半轴交于点C,与y轴的正半轴交于点B,直线BA与x轴的负半轴交于点A,AB=5OC,射线BN∥x轴.
如图,在坐标系中,直线y=-3x+6与x轴的正半轴交于点C,与y轴的正半轴交于点B,直线BA与x轴的负半轴交于点A,AB=5OC,射线BN∥x轴.分析 (1)根据直线y=-3x+6求得B、C的坐标,然后根据已知条件求得A点的坐标,即可利用待定系数法求得直线AB的解析式;
(2)先求得AB=AC=10,进而求得PB=BD=MC=t,然后分当0<t≤5时和5<t≤10时,分别讨论求得QD,根据三角形相似求得PE和MF,根据三角形面积公式即可求得S与t之间的函数关系式;
(3)先求得△PQM是等腰三角形,然后根据已知条件证得R是PM的中点,从而证得PM是⊙R的直径,得出△PQM是等腰直角三角形,作QG⊥OA,MH⊥AB于H,证得作QG⊥OA,MH⊥AB于H,根据角平分线的性质求得MH=MG=$\frac{4}{5}$t-(10-t)=$\frac{9}{5}$t-10,然后根据三角形相似即可求得t的值.
解答 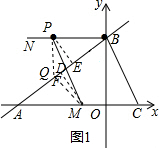 解:(1)∵直线y=-3x+6与x轴的正半轴交于点C,与y轴的正半轴交于点B,
解:(1)∵直线y=-3x+6与x轴的正半轴交于点C,与y轴的正半轴交于点B,
∴B(0,6),C(2,0),
∴OB=6,OC=2,
∵AB=5OC,
∴AB=10,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=8,
∴A(-8,0),
设直线AB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{b=6}\\{-8k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=6}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{3}{4}$x+6;
(2)∵OA=8,OC=2,
∴AC=10=AB,
∵BN∥x轴,PM∥BC,
∴MC=PB=t,
∴BD=MC=t,
∵AQ=t,
当0<t≤5时,如图1,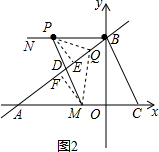
∴QD=10-2t,
作PE⊥AB于E,MF⊥AB于F,
∴∠AFO=∠AOB=90°,
∵∠OAB=∠MAF,
∴△AMF∽△ABO,
∴$\frac{MF}{OB}$=$\frac{AM}{AB}$,
∵AM=10-t,AB=10,OB=6,
∴$\frac{MF}{6}$=$\frac{10-t}{10}$,
∴MF=6-$\frac{3}{5}$t,
同理:PE=$\frac{3}{5}$t,
∴S=S△MQD+S△PQD=$\frac{1}{2}$QD•MF+$\frac{1}{2}$QD•PE=$\frac{1}{2}$×(10-2t)×6=30-6t;
即:S与t之间的函数关系式为S=-6t+30;
当5<t≤10时,如图2,
则QD=2t-10,
∴S=S△MQD+S△PQD=$\frac{1}{2}$QD•MF+$\frac{1}{2}$QD•PE=$\frac{1}{2}$×(2t-10)×6=6t-30;
综上:S=$\left\{\begin{array}{l}{30-6t(0<t≤5)}\\{6t-30(5<t≤10)}\end{array}\right.$;
(3)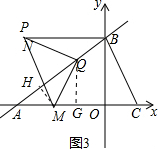 存在,
存在,
理由:∵PB=MC=AQ=t,AB=AC=10,
∴BQ=AM=10-t,
∵BN∥x轴,
∴∠PBQ=∠QAM,
在△PBQ和△QAM中,
$\left\{\begin{array}{l}{PB=AQ}\\{∠PBQ=∠QAM}\\{BQ=AM}\end{array}\right.$,
∴△PBQ≌△QAM(SAS),
∴PQ=QM,∠BPQ=∠AQM,
∵⊙R是△PQM的外接圆,
∴R在PM的垂直平分线上,
∵PR⊥QR,
∴R是PM的中点,
∴PM是⊙R的直径,
∴∠PQM=90°,
∴∠AQP+∠AQM=90°=∠BPQ+∠QBP+∠AQM=∠QAM+∠AQM+AQM=∠QAM+2∠AQM,
作QG⊥OA,MH⊥AB于H,
∵∠QAM+∠AQG=90°,
∴∠AQG=2∠AQM,
∴∠AQM=∠MQG,
∵QG∥OB,
∴$\frac{AG}{AO}$=$\frac{AQ}{AB}$,
即$\frac{AG}{8}$=$\frac{t}{10}$,
∴AG=$\frac{4}{5}$t,
∵AM=10-t,
∴MH=MG=$\frac{4}{5}$t-(10-t)=$\frac{9}{5}$t-10,
∵∠AHM=∠AOB=90°,∠MAH=∠BAO,
∴△AMH∽△ABO,
∴$\frac{MH}{OB}$=$\frac{AM}{AB}$,即$\frac{\frac{9}{5}t-10}{6}$=$\frac{10-t}{10}$,
解得t=$\frac{20}{3}$,
即当t=$\frac{20}{3}$时,使得PR⊥QR.
点评 本题是一次函数的综合题,考查了待定系数法求一次函数的解析式,平行四边形的性质,三角形相似的判定和性质,圆周角定理,三角形全等的判定和性质,角平分线的性质,熟练掌握性质定理是解题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
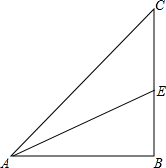 如图,在Rt△ABC的场地上,∠B=90°,AB=BC,∠CAB的平分线AE交BC于点E.甲、乙两人同时从A处出发,以相同的速度分别沿AC和A→B→E线路前进,甲的目的地为C,乙的目的地为E,请你判断一下,甲、乙两人谁先到达各自的目的地?请说明理由.
如图,在Rt△ABC的场地上,∠B=90°,AB=BC,∠CAB的平分线AE交BC于点E.甲、乙两人同时从A处出发,以相同的速度分别沿AC和A→B→E线路前进,甲的目的地为C,乙的目的地为E,请你判断一下,甲、乙两人谁先到达各自的目的地?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
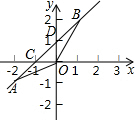 如图,已知一次函数y=kx+b的图象经过A(-2,-1)、B(1,2)两点,并且交x轴于点C,交y轴于点D.
如图,已知一次函数y=kx+b的图象经过A(-2,-1)、B(1,2)两点,并且交x轴于点C,交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=DE,BC=EF,∠A=∠D | B. | ∠A=∠D,∠C=∠F,AC=EF | ||
| C. | AB=DE,BC=EF,AC=DF | D. | ∠B=∠E |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com