等腰梯形两底差为8,高为4,则等腰梯形的锐角为________.
45°
分析:如图,梯形ABCD中,AD∥BC,AB=CD,作AE⊥BC,垂足为E,根据等腰梯形的性质可知BE=

×(BC-AD),证明△ABE为等腰直角三角形即可.
解答:如图,过点A作AE⊥BC,垂足为E,
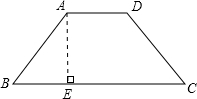
根据等腰梯形的性质可知,
BE=

×(BC-AD)=

×8=4=AE,
∴△ABE为等腰直角三角形,
∴∠B=45°.
故本题答案为:45°.
点评:本题考查了等腰梯形的性质,等腰直角三角形的性质.作梯形的高是梯形常用的作辅助线的方法,此时BE即为上下底差的一半.
