
(本题满分12分)如图,点 是半圆
是半圆 的半径
的半径 上的动点,作
上的动点,作 于
于 .点
.点 是半圆上位于
是半圆上位于 左侧的点,连结
左侧的点,连结 交线段
交线段 于
于 ,且
,且 .
.

(1)求证: 是⊙O的切线.
是⊙O的切线.
(2)若⊙O的半径为 ,
, ,设
,设 .
.
①求 关于
关于 的函数关系式.
的函数关系式.
②当 时,求
时,求 的值.
的值.
(1)见解析;(2)①y=x2+144②tanB= .
.
【解析】
试题分析:(1)连DO ,然后根据角的关系证明PD⊥OD即可;(2)①连接PO ,在Rt△PDO中用勾股定理表示出PO2,在Rt△PCO中再用勾股定理可得y与x的关系,化简即可;②把x= 代入①中函数关系式求出y的值,然后可分别求出线段EC=
代入①中函数关系式求出y的值,然后可分别求出线段EC= ,CB=3
,CB=3 ,然后根据正切的定义可解.
,然后根据正切的定义可解.
试题解析:(1)证明:连DO 1分
∵PC⊥BA
∴∠PCB=90°
∴∠3+∠4=90° 2分
又∵PD=PE OD=OB
∴∠1=∠2 ∠5=∠4
又∵∠2=∠3
∴∠1+∠5=90° 3分
∴∠PDO=90°
∴PD⊥OD
∴PD是QO切线 4分
(2)①连接PO
在Rt△PDO中PD2=y DC=4
∴PO2=y+(4 )2=y+48 5分
)2=y+48 5分
在Rt△PCO中OC=x PC=8
∴PO2=x2+(8 )2=x2+192 6分
)2=x2+192 6分
∴y+48=x2+192
∴y=x2+144 8分
②当x= 时,y=147
时,y=147
∴PD= =7
=7 9分
9分
∴PE=PD=7 10分
10分
∵PC=8
∴EC=8 -7
-7 =
=
又∵OC=X= ,OB=4
,OB=4
∴CB=3 11分
11分
在Rt△BCE中
tanB= =
=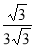 =
= 12分
12分
备注:以上各题有其他不同解法请对照评分标准相应给分。
考点:1.切线的判定;2.勾股定理;3.函数与几何知识的综合;4.锐角三角函数.
考点分析: 考点1:圆 圆,圆的有关性质与圆的有关计算是近几年各地中考命题的重点内容。题型以填空题,选择题和解答题为主,也有以阅读理解,条件开放,结论开放探索题作为新的题型,分值一般是6-12分,难易度为中,考察内容:①圆的有关性质的应用。垂径定理是重点。② 直线和圆,圆和圆的位置关系的判定及应用。③弧长,扇形面积,圆柱,圆锥的侧面积和全面积的计算④圆与相似三角形,三角函数的综合运用以及有关的开放题,探索题。突破方法:①熟练掌握圆的有关行政,掌握求线段,角的方法,理解概念之间的相互联系和知识之间的相互转化。②理解直线和原的三种位置关系,掌握切线的性质和判定的歌,会根据条件解决圆中的动态问题。③掌握有两圆半径的和或差与圆心距的大小关系来盘底的那个两个圆的位置关系,对中考试题中常出现的阅读理解题,探索题,要灵活运用圆的有关性质,进行合理推理与计算。④掌握弧长,扇形面积计算公式。⑤理解圆柱,圆锥的侧面展开图⑥对组合图形 的计算要灵活运用计算方法解题。 试题属性

科目:初中数学 来源:2014-2015学年山东省滨州市九年级下学期4月模拟数学试卷(解析版) 题型:选择题
据统计,我国2013年全年完成造林面积约6090000公顷。6090000用科学记数法可表示为( ).
A.6.09× B.6.09×
B.6.09×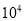 C.609×
C.609×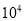 D.60.9×
D.60.9×
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省东港市九年级九校联考数学试卷(解析版) 题型:填空题
如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”。则半径为2的“等边扇形”的面积为 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省东港市九年级九校联考数学试卷(解析版) 题型:选择题
已知等腰三角形的一边等于3,一边等于6,则它的周长为( )
A、12 B、12或15 C、15 D、以上都不对
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市片九年级3月月考数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在△ABD和△ACE中,AB=AD,AC=AE,∠BAD=∠CAE,连接BC、DE相交于点F,BC与AD相交于点G.
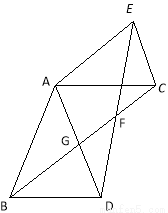
(1)求证:BC=DE;
(2)如果∠ABC=∠CBD ,那么线段FD是线段FG和FB的比例中项吗?为什么?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市片九年级3月月考数学试卷(解析版) 题型:填空题
已知一个圆锥底面圆的半径为6cm,高为8cm,则圆锥的侧面积为 cm2.(结果保留π)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片九年级下学期第一次月考数学试卷(解析版) 题型:解答题
((本题满分12分)
知识迁移
当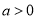 且
且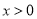 时,因为
时,因为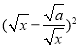 ≥
≥ ,所以
,所以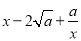 ≥
≥ ,
,
从而 ≥
≥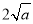 (当
(当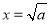 时取等号).
时取等号).
记函数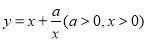 ,由上述结论可知:当
,由上述结论可知:当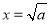 时,该函数有最小值为
时,该函数有最小值为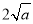 .
.
直接应用
已知函数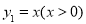 与函数
与函数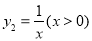 , 则当
, 则当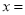 _________时,
_________时,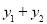 取得最小值为_________.
取得最小值为_________.
变形应用
已知函数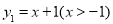 与函数
与函数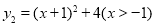 ,求
,求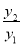 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的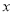 的值.
的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共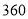 元;二是燃油费,每千米为
元;二是燃油费,每千米为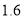 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为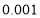 .设该汽车一次运输的路程为
.设该汽车一次运输的路程为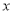 千米,求当
千米,求当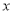 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com