练习册

  • 练习册
  • 试题
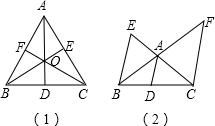
    精英家教网 > 初中数学 > 题目详情
    精英家教网利用塞瓦定理可以简便地证明重心定理、内心定理和垂心定理：
    分析：①由AD，BE，CF是△ABC的中线，根据中线的性质得到
    BD
    DC
    •
    CE
    CA
    •
    AF
    FB
    =1    ，得到AD，BE，CF三条中线交于一点．
    ②由AD，BE，CF是△ABC的内角平分线，根据角平分线定理得到
    BD
    DC
    =
    AB
    AC
    ，
    CE
    EA
    =
    BC
    AB
    ，
    AF
    FB
    =
    AC
    BC
    ．把它们分别相乘然后利用塞瓦定理，得到AD，BE，CF三条内角平分线交于一点．
    ③由AD，BE，CF是△ABC的三条高线，则△ABD∽△CBF，得到
    BD
    FB
    =
    AB
    BC
    ；△ACD∽△BCE，得到
    CE
    CD
    =
    BC
    AC
    ；△ABE∽△ACF，得到
    AF
    AE
    =
    AC
    AB
    ．把它们分别相乘然后利用塞瓦定理，得到AD，BE，CF三条高线或延长线交于一点．
    解答：证明：①如果AD，BE，CF是△ABC的中线，则BD=DC，CE=AE，AF=FB．
    ∴
    BD
    DC
    •
    CE
    CA
    •
    AF
    FB
    =1    ，
    ∴AD，BE，CF三条中线交于一点；

    ②如果AD，BE，CF是△ABC的内角平分线，
    则
    BD
    DC
    =
    AB
    AC
    ，
    CE
    EA
    =
    BC
    AB
    ，
    AF
    FB
    =
    AC
    BC
    ．
    ∴
    BD
    DC
    •
    CE
    EA
    •
    AF
    FB
    =
    AB
    AC
    •
    BC
    AB
    •
    AC
    BC
    =1    ，
    因此AD，BE，CF三条内角平分线交于一点；

    ③如果AD，BE，CF是△ABC的三条高线，
    ∵△ABD∽△CBF，
    ∴
    BD
    FB
    =
    AB
    BC
    ，
    ∵△ACD∽△BCE，
    ∴
    CE
    CD
    =
    BC
    AC
    ，
    ∵△ABE∽△ACF，
    ∴
    AF
    AE
    =
    AC
    AB
    ．
    ∴
    BD
    DC
    •
    CE
    EA
    •
    AF
    FB
    =
    BD
    FB
    •
    CE
    DC
    •
    AF
    EA
    =
    AB
    BC
    ．
    BC
    AC
    •
    AC
    AB
    =1，
    因此AD，BE，CF三条高线或延长线交于一点．
    点评：本题考查了塞瓦定理的运用．也考查了三角形中线、角平分线和高的性质以及三角形相似的性质．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    同步练习册答案