
 在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为
在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为
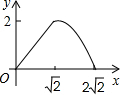

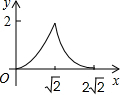
 ,OB=OD=
,OB=OD= BD=
BD= ,
, ,
, EF•BP=
EF•BP= ×2x×x=x2;
×2x×x=x2; <x≤2
<x≤2 ,
, =(2
=(2 -x):
-x): ,
, -x),
-x), EF•BP=
EF•BP= ×2(2
×2(2 -x)×x=-x2+
-x)×x=-x2+ x,
x,

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
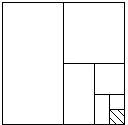 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com