
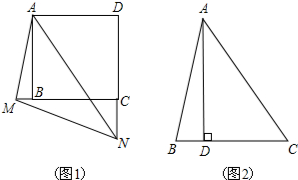
分析 (1)如图1,在CD上截取DE=MB,连接AE由正方形的性质就可以得出Rt△ABM≌Rt△ADE,就可以得出AM=AE,∠DAE=∠BAN,进而得出△ANM≌△ANE就可以得出结论;
(2)以AD为边作正方形ADEF,在EF上截取FQ=BD,就可以得出△ABD≌△AQF,得出∠CAQ=45°,∠BAC=∠CAQ,就有△BAC≌△QAC,从而得出BC=CQ=13,设AD=x,则QE=x-3,CE=x-10.由勾股定理就可以求出x的值,得出AD的值,由三角形的面积公式就可以求出结论.
解答 解:(1)如图1,在CD上截取DE=MB,连接AE.
∵四边形ABCD是正方形
∴AB=BC=AD,∠ABC=∠D=90°
在△ABM和△ADE中
$\left\{\begin{array}{l}{MB=ED}\\{∠ABM=∠ADE}\\{AB=AD}\end{array}\right.$,
∴△ABM≌△ADE(SAS),
∴∠BAM=∠DAE,AM=AE
∵∠MAN=45°
∴∠DAE+∠BAN=45°.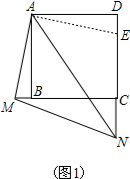
即∠NAE=45°.
在△ANM和△ANE中
$\left\{\begin{array}{l}{AM=AE}\\{∠MAN=∠EAN}\\{AN=AN}\end{array}\right.$,
∴△ANM≌△ANE(SAS),
∴S△AMN=S△AEN.
∵S△ADN=S△AEN+S△ADE,
∴S△ADN=S△ANE+S△ADE=S△AMN+S△ABM;
(2)以AD为边作正方形ADEF,在EF上截取FQ=BD.
在△ABD和△AQF中
$\left\{\begin{array}{l}{AD=AF}\\{∠ADB=∠F}\\{BD=QF}\end{array}\right.$,
∴△ABD≌△AQF(SAS),
∴AB=AQ,∠BAD=∠FAQ
∵∠BAC=45°
∴∠BAD+∠DAC=45°
∴∠DAC+∠FAQ=45°
即∠CAQ=45°
∴∠BAC=∠CAQ.
在△BAC和△QAC中
$\left\{\begin{array}{l}{AB=AQ}\\{∠BAC=∠CAQ}\\{AC=AC}\end{array}\right.$,
∴△BAC≌△QAC(SAS),
∴BC=CQ=BD+CD=13.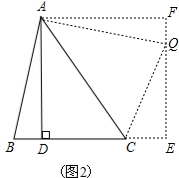
设AD=x,则QE=x-3,CE=x-10.
在Rt△CQE中,∠E=90°
∵CE2+QE2=CQ2
∴(x-10)2+(x-3)2=132
解得:x1=15,x2=-2(不合舍去)
∴AD=15
∴${S_{△ABC}}=\frac{1}{2}BC•AD=\frac{195}{2}$.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的性质的运用,解答时证明三角形全等是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段a和b,a>b,求作直角三角形ABC,使直角三角形的斜边AB=a,直角边AC=b.(用尺规作图,保留作图痕迹,不要求写作法)
如图,已知线段a和b,a>b,求作直角三角形ABC,使直角三角形的斜边AB=a,直角边AC=b.(用尺规作图,保留作图痕迹,不要求写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
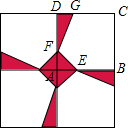 一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?
一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
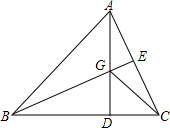 如图,在△ABC中,点D,E分别在BC,AC边上,E为AC的中点,AD,BE交于点G,BD=2DC,S△GEC=2,S△GDC=4,则△ABC的面积是( )
如图,在△ABC中,点D,E分别在BC,AC边上,E为AC的中点,AD,BE交于点G,BD=2DC,S△GEC=2,S△GDC=4,则△ABC的面积是( )| A. | 24 | B. | 30 | C. | 35 | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com