
 已知:如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,点D在边BC上,AE∥BC,AE=BD.
已知:如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,点D在边BC上,AE∥BC,AE=BD.分析 (1)根据等弧所对的圆周角相等,得出∠B=∠ACB,再根据全等三角形的判定得△ABD≌△CAE,即可得出AD=CE;
(2)连接AO并延长,交边BC于点H,由等腰三角形的性质和外心的性质得出AH⊥BC,再由垂径定理得BH=CH,得出CG与AE平行且相等.
解答 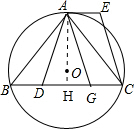 证明:(1)在⊙O中,
证明:(1)在⊙O中,
∵$\widehat{AB}$=$\widehat{AC}$,
∴AB=AC,
∴∠B=∠ACB,
∵AE∥BC,
∴∠EAC=∠ACB,
∴∠B=∠EAC,
在△ABD和△CAE中,$\left\{\begin{array}{l}{AB=CA}\\{∠B=∠EAC}\\{BD=AE}\end{array}\right.$,
∴△ABD≌△CAE(SAS),
∴AD=CE;
(2)连接AO并延长,交边BC于点H,
∵$\widehat{AB}$=$\widehat{AC}$,OA为半径,
∴AH⊥BC,
∴BH=CH,
∵AD=AG,
∴DH=HG,
∴BH-DH=CH-GH,即BD=CG,
∵BD=AE,
∴CG=AE,
∵CG∥AE,
∴四边形AGCE是平行四边形.
点评 本题考查了三角形的外接圆与外心以及全等三角形的判定和性质,平行四边形的判定,圆心角、弧、弦之间的关系,把这几个知识点综合运用是解题的关键.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
 平行四边形ABCD的两个顶点A、C在反比例函数y=$\frac{k}{x}$(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
平行四边形ABCD的两个顶点A、C在反比例函数y=$\frac{k}{x}$(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
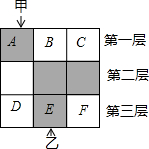 如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )| A. | 1<r<4 | B. | 2<r<4 | C. | 1<r<8 | D. | 2<r<8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
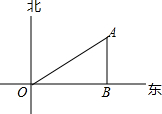 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )| A. | 250米 | B. | 250$\sqrt{3}$米 | C. | $\frac{500}{3}$$\sqrt{3}$米 | D. | 500$\sqrt{2}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 旅游人数 | 收费标准 |
| 不超过30人 | 人均收费80元 |
| 超过30人 | 每增加1人,人均收费降低1元,但人均收费不低于50元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com