
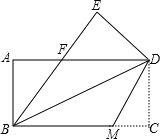
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
【答案】(1)证明见解析;(2)四边形式菱形,理由见解析.
【解析】试题分析:(1)因为△BCD关于BD折叠得到△BED,显然△BCD≌△BED,得出CD=DE=AB,∠E=∠C=∠A=90°.再加上一对对顶角相等,可证出△ABF≌△EDF
(2)利用折叠知识及菱形的判定可得出四边形BMDF是菱形.
试题解析:(1)由折叠可知,CD=ED,∠E=∠C.
在矩形ABCD中,AB=CD,∠A=∠C.
∴AB=ED,∠A=∠E.
∵∠AFB=∠EFD,
∴△AFB≌△EFD.
(2)四边形BMDF是菱形.
理由:由折叠可知:BF=BM,DF=DM.
由(1)知△AFB≌△EFD,
∴BF=DF.
∴BM=BF=DF=DM.
∴四边形BMDF是菱形.


科目:初中数学 来源: 题型:
【题目】用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为_____cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n-![]() ≤x<n+
≤x<n+![]() ,则(x)=n.如(0.46)=0,(3.67)=4.
,则(x)=n.如(0.46)=0,(3.67)=4.
给出下列关于(x)的结论:
①(1.493)=1;
②(2x)=2(x);
③若(![]() x-1)=4,则实数x的取值范围是9≤x<11;
x-1)=4,则实数x的取值范围是9≤x<11;
④当x≥0,m为非负整数时,有(m+2 017x)=m+(2 017x);
⑤(x+y)=(x)+(y).
其中,正确的结论有________(填写所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
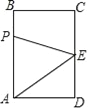
【题目】如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A﹣B﹣C﹣E运动,最终到达点E.若点P运动的时间为x秒,则当x=__时,△APE的面积等于5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A.2, ![]()
B.2,1
C.4, ![]()
D.4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别是ABCD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( ) 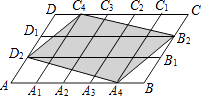
A.4
B.![]()
C.![]()
D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M. 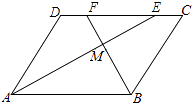
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com