
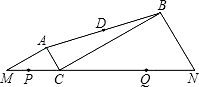
 如图,MN=8,点P、Q在线段MN上,且PM=1,NQ=2.C是线段MN上的动点,分别以CM、CN为斜边在线段MN的同侧作直角△ACM和直角△BCN,使∠AMC=∠BCN=30°,连接AB,设AB的中点为D,当点C从点P运动到点Q时,点D移动路径的长是
如图,MN=8,点P、Q在线段MN上,且PM=1,NQ=2.C是线段MN上的动点,分别以CM、CN为斜边在线段MN的同侧作直角△ACM和直角△BCN,使∠AMC=∠BCN=30°,连接AB,设AB的中点为D,当点C从点P运动到点Q时,点D移动路径的长是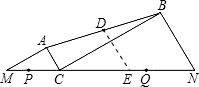 解:取CN的中点E,连接DE,设MC=x,1≤x≤6,
解:取CN的中点E,连接DE,设MC=x,1≤x≤6,| x |
| 2 |
| x |
| 2 |
| AC+BN |
| 2 |
| x |
| 2 |
| x |
| 2 |


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
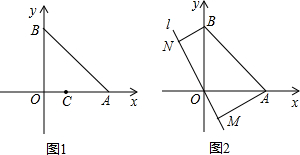 平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).
平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市黄梅县实验中学2010-2011学年八年级上学期综合能力测试第一次模拟数学试题 题型:044
如图,MN⊥AB于点D,AD=BD(即MN是AB的垂直平分线),则AC与BC的关系是_________.
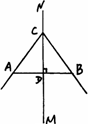
(1)先填空,再用一句简明的语言总结它的规律:_________.
(2)用(1)的结论证明下题:如图,在△ABC中,∠ABC的平分线BN与AC的垂直平分线MN相交于点N,过N分别作ND⊥AB交BA的延长线于点D,NE⊥BC于点E,求证:AD=CE.
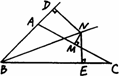
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
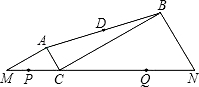 如图,MN=8,点P、Q在线段MN上,且PM=1,NQ=2.C是线段MN上的动点,分别以CM、CN为斜边在线段MN的同侧作直角△ACM和直角△BCN,使∠AMC=∠BCN=30°,连接AB,设AB的中点为D,当点C从点P运动到点Q时,点D移动路径的长是________.
如图,MN=8,点P、Q在线段MN上,且PM=1,NQ=2.C是线段MN上的动点,分别以CM、CN为斜边在线段MN的同侧作直角△ACM和直角△BCN,使∠AMC=∠BCN=30°,连接AB,设AB的中点为D,当点C从点P运动到点Q时,点D移动路径的长是________.查看答案和解析>>
科目:初中数学 来源:2011年江苏省南京市鼓楼区中考数学二模试卷(解析版) 题型:填空题
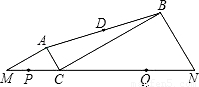
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com