
分析 ①将已知点的坐标代入反比例函数的解析式即可求得k值;
②根据确定的k的符号判断其所在的象限和增减性;
③利用描点作图法作出图象即可;
④满足函数关系式即在,否则不在.
解答 解:①∵反比例函数y=$\frac{1-k}{x}$的图象经过点A(2,-4),
∴1-k=2×(-4)=-8;
解得:k=9;
②∵k=-8<0,
∴图象位于二、四象限,在每个象限内y随x的增大而增大;
③图象为: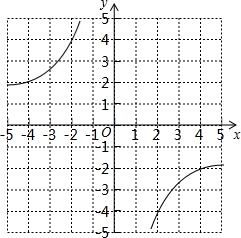
④∵-2×4=-8、
-1×5=-5≠-8,
∴B(-2,4)在反比例函数的图象上,C(-1,5)不在反比例函数的图象上.
点评 本题考查了反比例函数的图象及性质,解题的关键是正确的求得反比例函数的解析式,难度不大.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
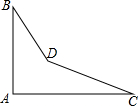 如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?
如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
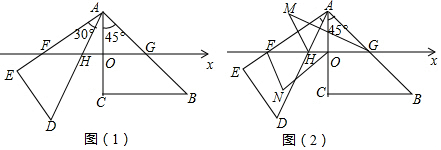
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
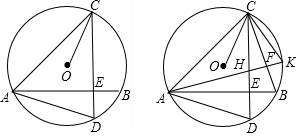
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1或$\sqrt{3}$ | B. | 1或2$\sqrt{3}$ | C. | 2或$\sqrt{3}$ | D. | 2或2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D.则阴影部分面积为(结果保留π)( )
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D.则阴影部分面积为(结果保留π)( )| A. | 24-4π | B. | 32-4π | C. | 32-8π | D. | 24-2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com