
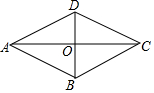
 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且AC⊥BD,若AB=5 cm,DO=3cm,则△ADC的周长为18cm.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且AC⊥BD,若AB=5 cm,DO=3cm,则△ADC的周长为18cm. 分析 证明四边形ABCD是菱形,得出CD=AD=AB=5cm,由勾股定理求出OA=4cm,得出AC=8cm,即可得出答案.
解答 解:∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,OA=OC=$\frac{1}{2}$AC,
∴CD=AD=AB=5cm,
∴OA=$\sqrt{A{D}^{2}-D{O}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4(cm),
∴AC=2OA=8cm,
∴△ADC的周长为AD+CD+AC=5+5+8=18(cm);
故答案为:18.
点评 本题考查平行四边形性质.菱形的判定与性质、勾股定理、三角形周长等知识,证明四边形ABCD是菱形是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
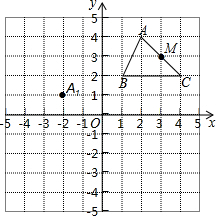 如图,在平面直角坐标系中,是边长为1的正方形网格,△ABC的顶点均在图中网格的格点上,M为AC中点.
如图,在平面直角坐标系中,是边长为1的正方形网格,△ABC的顶点均在图中网格的格点上,M为AC中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
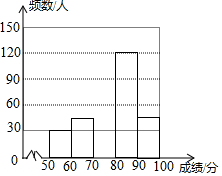 为了弘扬苏州优秀传统文化,某中学举办了苏州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分.赛后对全体参赛选手的成绩进行统计后,绘制了图中两幅不完整的答题情况的统计图.
为了弘扬苏州优秀传统文化,某中学举办了苏州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分.赛后对全体参赛选手的成绩进行统计后,绘制了图中两幅不完整的答题情况的统计图. | 成绩分组 (x/分) | 频数(人) | 频率 |
| 50≤x<60 | 30 | 0.10 |
| 60≤x<70 | 45 | a |
| 70≤x<80 | b | 0.20 |
| 80≤x<90 | 120 | 0.40 |
| 90≤x<100 | 45 | 0.15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com