练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    等边△ABC的周长为6，则等边△ABC的面积是________．


    分析：根据等边三角形三线合一的性质，可求得D为BC中点且AD⊥BC，根据勾股定理即可求AD的值，根据AD、BC即可计算△ABC的面积．
    解答：周长为6，则等边△ABC的边长为2，
    ∵AD为BC边上的高，则D为BC的中点，

    ∴BD=DC=1，∴AD==，
    ∴等边△ABC的面积=BC•AD=×2×=，
    故答案为．
    点评：本题考查了等边三角形三线合一的性质，考查了勾股定理在直角三角形中的运用，考查了三角形面积的计算，本题中根据勾股定理计算AD的长是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    等边△ABC的周长为12cm，则它的面积为
     
    cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

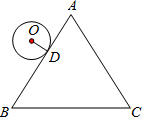    （2012•北海）如图，等边△ABC的周长为6π，半径是1的⊙O从与AB相切于点D的位置出发，在△ABC外部按顺时针方向沿三角形滚动，又回到与AB相切于点D的位置，则⊙O自转了（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知等边△ABC的周长为6厘米，求它的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

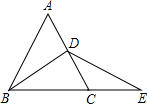    精英家教网如图，已知等边△ABC的周长为6，BD是AC边的中线，E为BC延长线上一点，CD=CE，那么△BDE的周长是（　　）
    A、5+2
    		3
    B、5+
    		3
    C、3+2
    		3
    D、3+
    		3

    查看答案和解析>>

    科目：初中数学 来源：2012年初中毕业升学考试（广西北海卷）数学（解析版） 题型：选择题

    如图，等边△ABC的周长为6π，半径是1的⊙O从与AB相切于点D的位置

    出发，在△ABC外部按顺时针方向沿三角形滚动，又回到与AB相切于点D的位置，则⊙O自转了：【    】

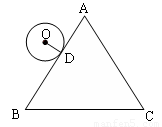
    A．2周          B．3周          C．4周          D．5周

     

    查看答案和解析>>

    同步练习册答案