
某水果店销售某中水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)的变化趋势,每千克成本y2(元)与销售时间第x月满足函数关系式y2=mx2﹣8mx+n,其变化趋势如图2.

(1)求y2的解析式;
(2)第几月销售这种水果,每千克所获得利润最大?最大利润是多少?
(1) y2=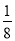 x2﹣x+
x2﹣x+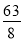 (1≤x≤12);(2) 第3月销售这种水果,每千克所获得利润最大,最大利润是
(1≤x≤12);(2) 第3月销售这种水果,每千克所获得利润最大,最大利润是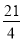 元/千克.
元/千克.
【解析】
试题分析:(1)把函数图象经过的点(3,6),(7,7)代入函数解析式,解方程组求出m、n的值,即可得解;
(2)根据图1求出每千克的售价y1与x的函数关系式,然后根据利润=售价﹣成本得到利润与x的函数关系式,然后整理成顶点式形式,再根据二次函数的最值问题解答即可.
试题解析:(1)由图可知,y2=mx2﹣8mx+n经过点(3,6),(7,7),
∴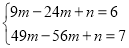 ,
,
解得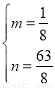 .
.
∴y2=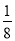 x2﹣x+
x2﹣x+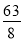 (1≤x≤12);
(1≤x≤12);
(2)设y1=kx+b(k≠0),
由图可知,函数图象经过点(4,11),(8,10),
则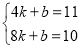 ,
,
解得 ,
,
所以,y1=﹣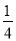 x+12,
x+12,
所以,每千克所获得利润=(﹣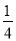 x+12)﹣(
x+12)﹣(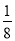 x2﹣x+
x2﹣x+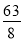
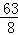 )
)
=﹣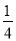 x+12﹣
x+12﹣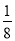 x2+x﹣
x2+x﹣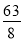
=﹣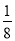 x2+
x2+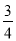 x+
x+
=﹣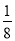 (x2﹣6x+9)+
(x2﹣6x+9)+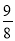 +
+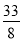
=﹣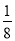 (x﹣3)2+
(x﹣3)2+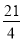 ,
,
∵﹣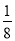 <0,
<0,
∴当x=3时,所获得利润最大,为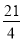 元.
元.
答:第3月销售这种水果,每千克所获得利润最大,最大利润是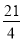 元/千克.
元/千克.
【考点】二次函数的应用.


科目:初中数学 来源:2014年初中毕业升学考试(贵州黔西卷)数学(解析版) 题型:填空题
如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=35°,则∠2的度数为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:选择题
“横看成岭侧成峰”从数学的角度解释为( )
A.从不同的方向观察同一建筑物时,看到的图形不一样
B.从同一方向观察同一建筑物时,看到的图形不一样
C.从同一的方向观察不同的建筑物时,看到的图形一样
D.以上答案都不对
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:选择题
某商场对上月笔袋销售的情况进行统计如下表所示:
颜色 | 白色 | 黄色 | 蓝色 | 紫色 | 红色 |
数量(个) | 56 | 128 | 520 | 210 | 160 |
经理决定本月进笔袋时多进一些蓝色的,经理的这一决定应用了哪个统计知识( )
A.平均数 B.方差 C.中位数 D.众数
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建三明卷)数学(解析版) 题型:选择题
PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
A.0.25×10-5 B.2.5×10-5 C.2.5×10-6 D.2.5×10-7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com