
射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,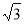 cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)

t=2或3≤t≤7或t=8.
【解析】
试题分析:∵△ABC是等边三角形,
∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,
∵QN∥AC,AM=BM.∴N为BC中点,∴MN=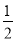 AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,
AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,
分为三种情况:①如图1,
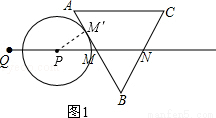
当⊙P切AB于M′时,连接PM′,则PM′=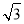 cm,∠PM′M=90°,
cm,∠PM′M=90°,
∵∠PMM′=∠BMN=60°,∴M′M=1cm,PM=2MM′=2cm,∴QP=4cm﹣2cm=2cm,即t=2;
②如图2,
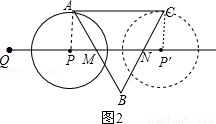
当⊙P于AC切于A点时,连接PA,则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=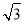 cm,
cm,
∴PM=1cm,∴QP=4cm﹣1cm=3cm,
即t=3,
当⊙P于AC切于C点时,连接P′C,
则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=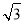 cm,∴P′N=1cm,
cm,∴P′N=1cm,
∴QP=4cm+2cm+1cm=7cm,
即当3≤t≤7时,⊙P和AC边相切;
③如图3,
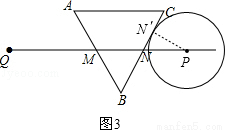
当⊙P切BC于N′时,连接PN′,则PN′=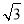 cm,∠PN′N=90°,
cm,∠PN′N=90°,
∵∠PNN′=∠BNM=60°,∴N′N=1cm,PN=2NN′=2cm,∴QP=4cm+2cm+2cm=8cm,
即t=8;
故答案为:t=2或3≤t≤7或t=8.
考点:1.切线的性质;2.等边三角形的性质;3.分类讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年江苏省江阴市青阳片九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列说法不正确的是( )
A.半圆(或直径)所对的圆周角是直角
B.等边三角形的重心与外心重合
C.相等的弧所对的圆心角相等
D.平分弦的直径垂直于弦
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市青阳片九年级上学期期中考试数学试卷(解析版) 题型:选择题
李老师从“淋浴龙头”受到启发.编了一个题目:
在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A,B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM与x轴交于点N(n,0),如图3.当 时,求n的值.你解答这个题目得到的n值为( )
时,求n的值.你解答这个题目得到的n值为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市海陵区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)在等腰△ABC中,三边分别为 其中
其中 =5,若关于
=5,若关于 的方程
的方程 有两个相等的实数根,求△ABC的周长.
有两个相等的实数根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省附属初级中学九年级上学期期中考试数学试卷(解析版) 题型:填空题
已知△ABC∽△DEF,如果∠A=75°,∠B=25°,则∠F=______.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市海陵区九年级上学期期中考试数学试卷(解析版) 题型:选择题
直线l与圆心O的距离为6,半径r=5,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com