
已知:如图,△ABC中,点D、E是边AB上的点,CD平分∠ECB,且 .
.
(1)求证:△CED∽△ACD;
(2)求证: .
.
科目:初中数学 来源: 题型:填空题
如图所示,正方形ABCD的边长为2,点E、F分别为边AB、AD 的中点,点G是CF上的一点,使得3 CG =2 GF,则三角形BEG的面积为 .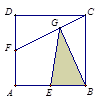
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
(1)求证:AP=AO;
(2)求证:PE⊥AO;
(3)当AE= AC,AB=10时,求线段BO的长度.
AC,AB=10时,求线段BO的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值
.(这个比值
叫做AE与AB的黄金比.)
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在数学课上,同学们研究图形的拼接问题.
比如:两个全等的等腰直角三角形纸片既能拼成一个大的等腰直角三角形(如图1),也能拼成一个正方形(如图2).
(1)现有两个相似的直角三角形纸片,各有一个角为 ,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;
,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;
(2)现有一个矩形恰好由三个各有一个角为 的直角三角形纸片拼成,请你画出两种不同拼法的示意图.在拼成这个矩形的三角形中,若每种拼法中最小的三角形的斜边长为
的直角三角形纸片拼成,请你画出两种不同拼法的示意图.在拼成这个矩形的三角形中,若每种拼法中最小的三角形的斜边长为 ,请直接写出每种拼法中最大三角形的斜边长.
,请直接写出每种拼法中最大三角形的斜边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com