
| 票得种类 | 夜票(A) | 平日普通票(B) | 指定日普通票(C) |
| 单价(元/张) | 60 | 100 | 150 |
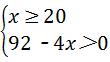 解得,
解得,

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
 ,OA=1,OC=2,
,OA=1,OC=2, 点D在边OC上且
点D在边OC上且 .
. y轴上
y轴上 是否存在点P,直线PD与矩形对角线AC交于点M,使得
是否存在点P,直线PD与矩形对角线AC交于点M,使得 为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由. 抛物线
抛物线 经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且
经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且 沿DE折叠后点O落在边AB上
沿DE折叠后点O落在边AB上 处?
处?
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 交于y轴与点E,交AB于点F
交于y轴与点E,交AB于点F
 时,求证:∠BEF=∠BAO
时,求证:∠BEF=∠BAO查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
| 挪动珠子数(颗) | 2 | 3 | 4 | 5 | 6 | …… |
| 对应所得分数(分) | 2 | 6 | 12 | 20 | 30 | …… |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com