(1)解:当x=0时,y=4k,
当y=0时,x=-4,
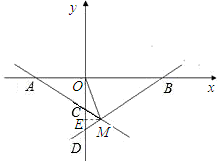
∴A(-4,0)C(0,4k),
由图象可知k<0
∴OA=4,OC=-4k,
∴
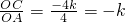
,
答:
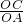
的值是-k.
(2)解:∵
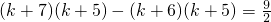
解得:

,
∴直线AC的解析式为:
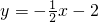
当x=2时,y=-3,
∴M(2,-3),
过点M作ME⊥y轴于E
∴ME=2
∵S
△BOM=3S
△DOM∴S
△BOD=4S
△DOM又∵

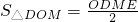
∴
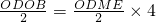
∴OB=4ME
∴OB=8
∴B(8,0),
设直线BD的解析式为:y=kx+b,
把B(8,0),M(2,-3)代入得:
则有
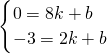
,
解得

,
∴直线BD的解析式为:
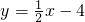
,
答:直线BD的解析式为:
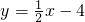
.
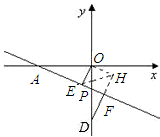
(3)解:②
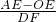
值不变.理由如下:
过点O作OH⊥DF交DF的延长线于H,连接EH,
∵DF⊥AP
∴∠DFP=∠AOP=90°
又∠DPF=∠APO
∴∠ODH=∠OAE
∵点D在直线
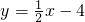
∴D(0,-4)
∴OA=OD=4
又∵∠OHD=∠OEA=90°
∴△ODH≌△OAE(AAS),
∴AE=DH,OE=OH,∠HOD=∠EOA
∴∠EOH=∠HOD+∠EOD=∠EOA+∠EOD=90°,
∴∠OEH=45°
∴∠HEF=45°=∠FHE
∴FE=FH
∴等腰Rt△OHE≌等腰Rt△FHE
∴OE=OH=FE=HF
∴
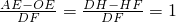
,
分析:(1)把x=0和y=0分别代入解析式即可求出点A、C的坐标,即可得到答案;
(2)解方程(k+7)(k+5)-(k+6)(k+5)=

,求出k的值,根据已知S
△BOM=3S
△DOM,能求出B的坐标,设直线BD的解析式为:y=kx+b,代入B、M的坐标即可得到答案;
(3)②不变,过点O作OH⊥DF交DF的延长线于H,连接EH,根据解析式求出D的坐标,根据AAS证△ODH≌△OAE,得到AE=DH,OE=OH,∠HOD=∠EOA,再证等腰Rt△OH≌等腰Rt△FHE,即可推出OE=OH=FE=HF,代入②即可求出答案.
点评:本题主要考查对一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,全等三角形的性质和判定等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,此题是一个综合性很强的题目,有一定的难度,但题型较好.

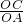 的值(用含有k的式子表示.);
的值(用含有k的式子表示.); 的根,求直线BD的解析式.
的根,求直线BD的解析式.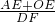 值不变;②
值不变;②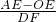 值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值.
值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值. .
. (1)解:当x=0时,y=4k,
(1)解:当x=0时,y=4k,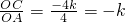 ,
,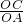 的值是-k.
的值是-k.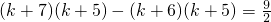
 ,
,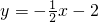

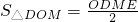
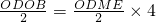
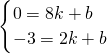 ,
, ,
,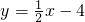 ,
,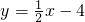 .
. (3)解:②
(3)解:② 值不变.理由如下:
值不变.理由如下: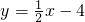
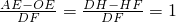 ,
, ,求出k的值,根据已知S△BOM=3S△DOM,能求出B的坐标,设直线BD的解析式为:y=kx+b,代入B、M的坐标即可得到答案;
,求出k的值,根据已知S△BOM=3S△DOM,能求出B的坐标,设直线BD的解析式为:y=kx+b,代入B、M的坐标即可得到答案;

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案 .
.